Предмет: Алгебра,
автор: Zoih
Решить систему срочно
Приложения:
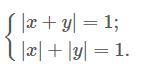
Ответы
Автор ответа:
1
Ответ:
Пары вида (x, -1-x), где x∈[-1; 0]
Пары вида (x, 1-x), где x∈[0; 1]
Объяснение:
Рассмотрим несколько случаев зависимо от знаков неизвестных.
Первый: x≥0 и y≥0. Тогда однозначно x+y≥0
Второй: x<0 и y<0. Тогда однозначно x+y<0
Третий: x≥0 и y<0. Здесь однозначно говорить о знаке суммы невозможно.
Пускай |x| ≥ |y|, тогда x+y≥0
Решений нет, поскольку y = 0 < 0 — неправильно.
Пускай |x| < |y|, тогда x+y<0
При таких ограничениях решением будет пара (0; -1)
Последний, четвертый случай: x<0 и y≥0. Также разобьем на два подслучая.
Пускай |x| < |y|, тогда x+y>0
Решений нет, поскольку x = 0 < 0 — неправильно.
Пускай |x| ≥ |y|, тогда x+y≤0
При таких ограничениях решением будет пара (-1; 0).
Осталось объединить решения и записать окончательный ответ.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Kotik652RG
Предмет: Французский язык,
автор: java5
Предмет: Геометрия,
автор: murad92
Предмет: Математика,
автор: 123diana123diana123