Предмет: Геометрия,
автор: cptleonn
Не понимаю как решать такую систему уравнений методом подстановки, если в уравнении только одно число, то как его решать?
Я встал в ступор, как только выразил R в первом уравнении.
R = r + 8 , и что дальше?
Приложения:
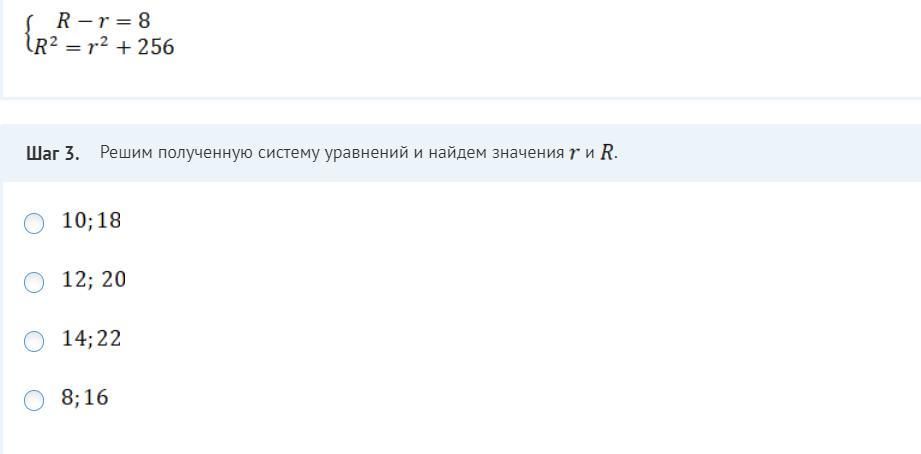
cos20093:
А переписать второе в виде (R-r)(R+r)=256 и подставить R-r=8 никак?
а что это даст? никакого упрощения...
интересно :) я продолжу еще на один ход, ладно? R+r=32. Заметно упрощение? Если нет, то тогда еще один ход. (R+r)+(R-r) = 32+8=40
не мучайся, по-любому надо выразить R от r (или наоборот), возвести в квадрат и сунуть во второе уравнение...
я вроде уже ответ получил, странно... вы ребята из какого измерения?
Я запишу следующий ход :) вдруг станет понятно? 2R=40 R=20 r=20-8=12
ну правильно, ответ ты получишь, но за большее число шагов... Я ж не говорю, что твой расклад неверный, а что он не упрощает логику....
Ответы
Автор ответа:
1
Ответ:
r²+16r+64=r²+256, 16r=192, r=12, R=20
Автор ответа:
1
Ответ:
r = 12, R = 20
Объяснение:
Название метода подстановки само за себя говорит, что выражение одной переменной через другую нужно подставить во второе уравнение и решать новое уравнение уже с одной переменной.
Похожие вопросы
Предмет: Русский язык,
автор: AlinaSad8090
Предмет: Русский язык,
автор: лучик7
Предмет: Қазақ тiлi,
автор: жазира4
Предмет: Английский язык,
автор: ВалерияГигаПашкина