Предмет: Геометрия,
автор: pilel
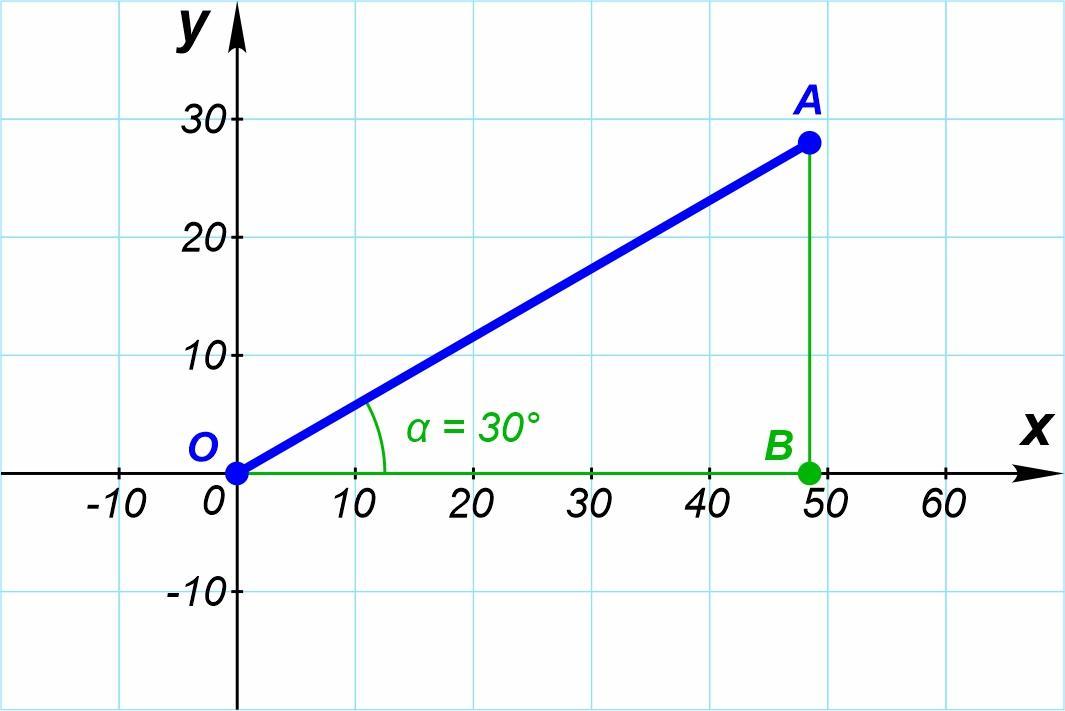
Дан угол α = 30°, который луч OA образует с положительной полуосью Ox, длина отрезка OA = 56.
Определи координаты точки A.
Ответы
Автор ответа:
0
Ответ:
Координаты точки A
Объяснение:
Рассмотрим Δ OAB:
Это прямоугольный треугольник, у которого ∠AOB = α = 30°
OA - гипотенуза = 56
Чтобы вычислить координату точки А по оси x, нужно найти длину катета OB:
Чтобы вычислить координату точки А по оси y, нужно найти длину катета AB:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: аня1178
Предмет: Қазақ тiлi,
автор: aiim5
Предмет: Русский язык,
автор: андре777
Предмет: Биология,
автор: Trolka02
Предмет: Литература,
автор: Nikitosbarbos44