Предмет: Геометрия,
автор: ilasluginov
В треугольнике, заданном вершинами А(-1;6;1), B(6;5;-1), С(3;2;1) найти угол A , АВ, ВС;
ДАЮ 35 БАЛОВ
Приложения:
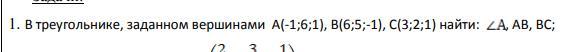
Ответы
Автор ответа:
0
Ответ:
∠A ≈ 40°; AB = √54 ≈ 7.348; BC = √22 ≈ 4.690;
Объяснение:
Дано:
ΔАВС
А(-1; 6; 1); В(6; 5; -1); С(3; 2; 1)
Найти:
∠А; АВ и ВС
Решение:
Найдём стороны треугольника
Проекции векторов АВ (7; -1; -2) и АС(4; -4; 0)
Скалярное произведение векторов
АВ · АС = 7 · 4 + 1 · 4 - 2· 0 = 32
Скалярное произведение
АВ · АС = АВ · АС · cos A = √54 ·√32 · cos A = 32
cos A ≈ 0.7698
∠A ≈ 40°
Похожие вопросы
Предмет: Русский язык,
автор: настя100200
Предмет: Русский язык,
автор: ксения08112003
Предмет: Английский язык,
автор: bagi11
Предмет: Математика,
автор: olinok78
Предмет: Окружающий мир,
автор: dedmakyanp7p5wd