Предмет: Математика,
автор: wyxrb
Найдите значение производной сложной функции в точке хо:
Приложения:
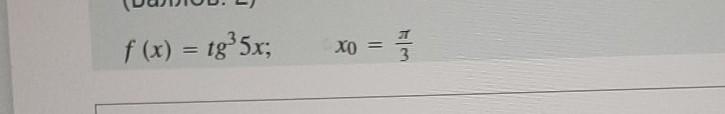
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: mama29
Предмет: Английский язык,
автор: alenagolikova42
Предмет: Немецкий язык,
автор: Аноним
Предмет: Окружающий мир,
автор: Лена9876
Предмет: Русский язык,
автор: neonunicorn