найди стороны паралелаграмма если его P=36 помогите пж
Ответы
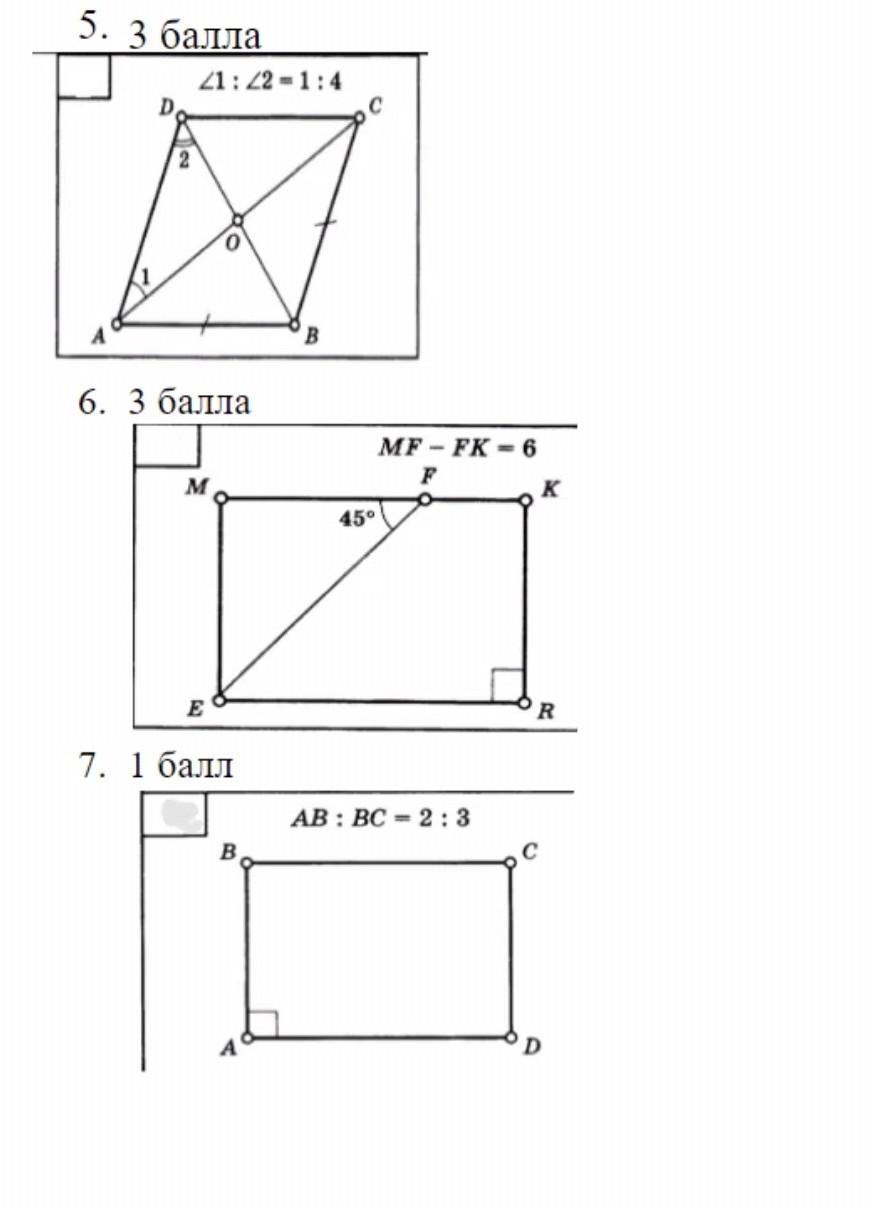
1) Это ромб , тк АВ=ВС. Все остальные стороны равны.
36:4=9 см одна сторона.
2)ΔMEF прямоугольный с одним углом 45. Р=36 , Р\2=р=36:2=18= МЕ+МК.
18= МЕ+МК=МЕ+(MF+FK)= МЕ+(MF-6) , МЕ+(MF-6) =18 ,МЕ=24-MF-6 .
∠Е=90-45=45° ⇒ ΔMEF прямоугольный и равнобедренный ⇒
МЕ=MF =х , ⇒ х=24-х-6 ⇒ х=9 ⇒ МЕ=MF=9 см ⇒ МК=9+6=15 см
3)
АВ=2х, ВС=3х
Р=2(АВ+ВС)
36=2(2х+3х)
18=5х
х=3,6 ⇒ АВ=2*3,6=7,2 , ВС=3*3,6=10,8
1,
У параллелограмма противоположные стороны равны, значит,
AB=DC и BC=AD
Но по условию АВ=ВС, значит,
AB=DC=BC=AD.
Пусть длина каждой стороны равна х, тогда периметр равен 4х,
а по условию он равен 36.
Получаем уравнение:
4х = 36
х = 36 : 4
х = 9 это и есть длина каждой стороны.
Ответ: 9; 9; 9; 9.
2.
1) По условию MF - FK = 6
Отсюда получаем: FK = MF - 6,
2) Найдём сторону MK.
МК = MF + FK
3) У параллелограмма противоположные углы равны, значит,
∠R = ∠M = 90°
Рассмотрим ΔMEF.
У него ∠M=90°
∠MFE = ∠MEF = 45°
Значит, ΔMEF - равнобедренный, => ME=MF
4) Пусть х - это длина стороны МЕ, тогда из равенства МК = MF + FK получаем
МК = х + (х-6)
(2х-6) - длина стороны МК
5) Так как у параллелограмма противоположные стороны равны, то его периметр равен:
2х + 3·(2х-6)
а по условию он равен 36.
Получаем уравнение:
2х + 2·(2х-6) = 36
2х + 4х -12= 36
6х = 36 + 12
х = 48 : 6
х = 8 - это длина каждой из сторон МЕ и KR
2 · 8 - 6 = 10 длина каждой из сторон МK и ER
Ответ: 8; 10 8; 10.
3.
AB : BC =2 : 3
Пусть 2х - длина каждой из сторон АВ и СD
3х - длина каждой из сторон АD и BC
тогда периметр равен: 2·2х + 2·3х , а по условию он равен 36.
Получаем уравнение:
4х + 6х = 36
10х = 36
х = 36 : 10
х = 3,6
2 · 3,6 = 7,2 - длина каждой из сторон АВ и СD
3 · 3,6 = 10,8 - длина каждой из сторон АD и BC
Ответ: 7, 2; 10,8; 7, 2; 10,8.