очень надо!!! даю 20 баллов

Ответы
Ответ:
Пошаговое объяснение:
Решение.
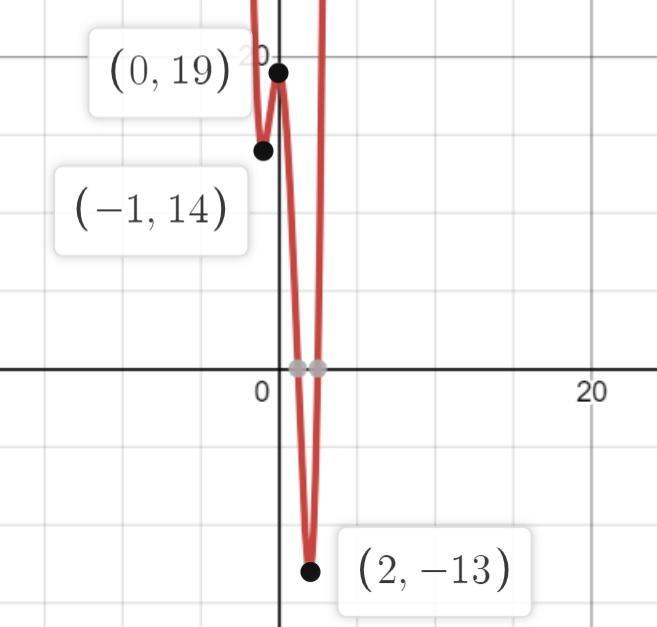
f(x)=3x^4-4x^3-12x^2+19;
Находим производную от х:
f'(x)=d(3x^4-4x^3-12x^2+19)/dx=d(3x^4)dx-d(4x^3)dx-d(12x^2)dx+d(19)dx=
=3dx^4dx-4x^3dx-12dx^2dx=3*4x^3-4*3x^2-2*12x=12x^3-12x^2-24x=
=12x(x^2-x-2);
Приравниваем к нулу: f'(x)=0;
12x(x^2-x-2)=0;
12x=0;
x1=0;
x²-x-2=0;
По т. Виета
x1+x2=1; x1*x2=-2;
x1=-1; x2=2;
Разложим полученное выражение на множители:
12x(x+1)(x-1) => в т. x=0 производная меняет знак с плюса на минус. Следовательно эта точка является наибольшим значением функции f(x)=3x^4-4x^3-12x^2+19.
f(0)=0-0-0+19 = 19. (См. скриншот)
--------------------------------
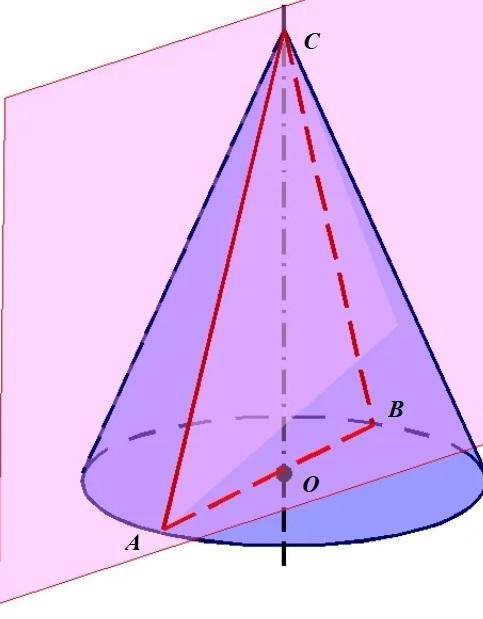
Осевое сечение конуса - треугольник АВС, у которого BC=17 - гипотенуза, ОВ=8 - катет. (См. скриншот).
Найдем высоту треугольника.
По т. Пифагора
СО=√17²-8²= √289-64=√225=15. Тогда
площадь осевого сечения
S=1/2*(2*8)*15=8*15=120.