Предмет: Математика,
автор: abdullintimur2046
Помогите пожалуйста, объясните почему -2 , прям очень подробно пожалуйста
Приложения:
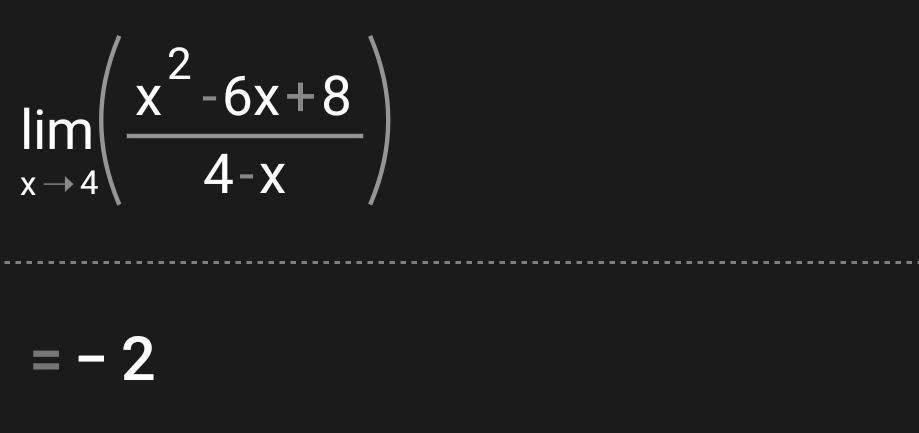
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
LymarIvan:
да как ещё подробнее?))
Не знаю)
сначала вот разложил числитель на множители
приравнял его к нулю, нашел корни и разложил
Ладно, спасибо)
потом в знаменателе вынес минус: 4- x = -(-4+x) = -(x-4)
теперь можно сократить
все, деления на ноль больше нет
Ойойой
осталось просто подставить 4, к которой стремится икс
Автор ответа:
1
раскладываем числитель на множители:
x²-6x+8=(x-4)(x-2)
тогда исходный предел примет вид:
Похожие вопросы
Предмет: Русский язык,
автор: mmmmm4
Предмет: Английский язык,
автор: poldina80
Предмет: Окружающий мир,
автор: синдр
Предмет: Русский язык,
автор: lezgin383838
Предмет: Українська література,
автор: 1968jsvp7r1qy