Предмет: Алгебра,
автор: birocoh405
Помогите прошу
35 баллов
Приложения:
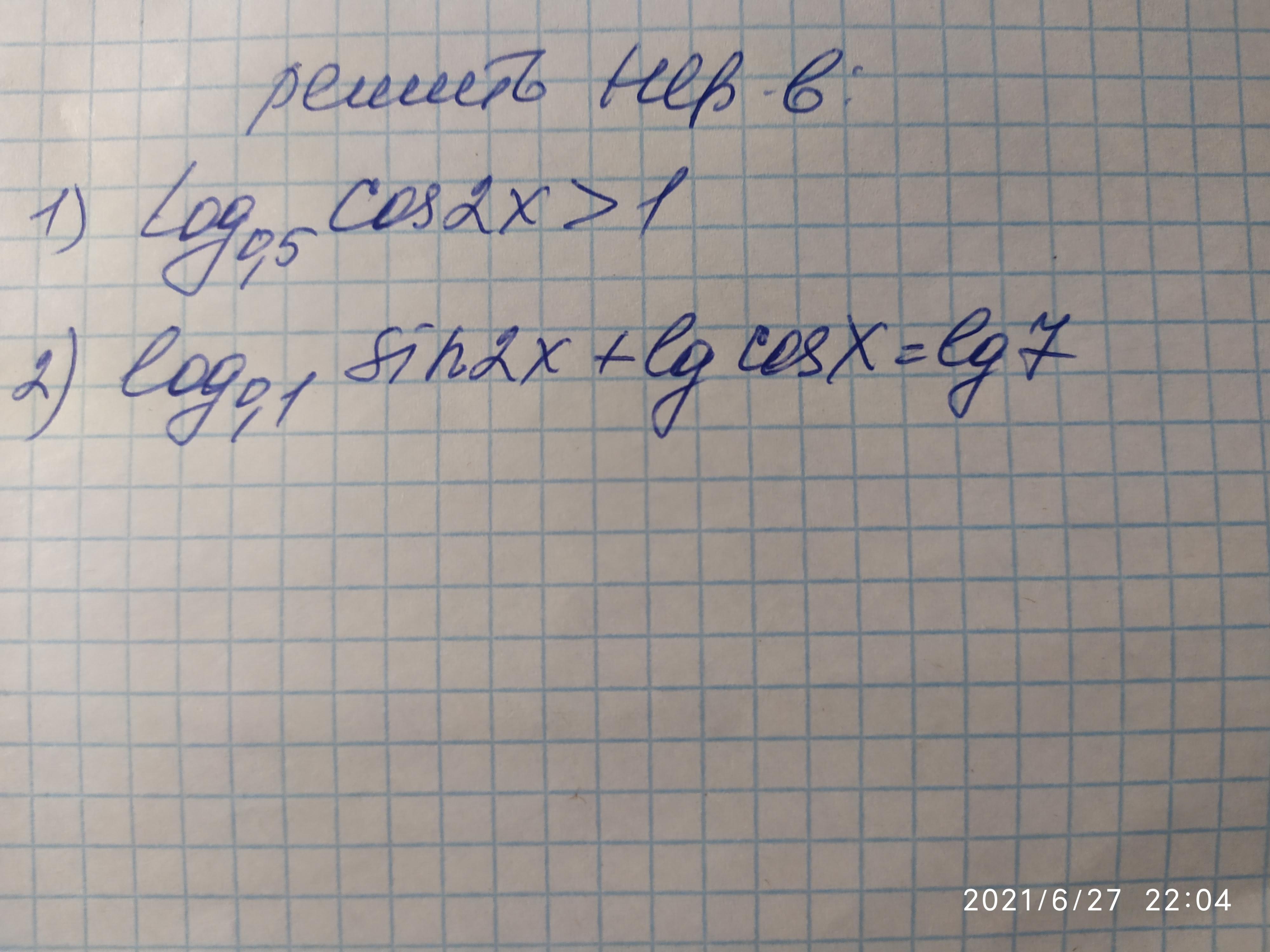
Ответы
Автор ответа:
0
Ответ.
C учётом ОДЗ:
C учётом ОДЗ:
Похожие вопросы
Предмет: Английский язык,
автор: poldina80
Предмет: Окружающий мир,
автор: синдр
Предмет: Русский язык,
автор: Алекдалср
Предмет: Українська література,
автор: 1968jsvp7r1qy
Предмет: Русский язык,
автор: F3ren9d