Предмет: Алгебра,
автор: sneghomina2004
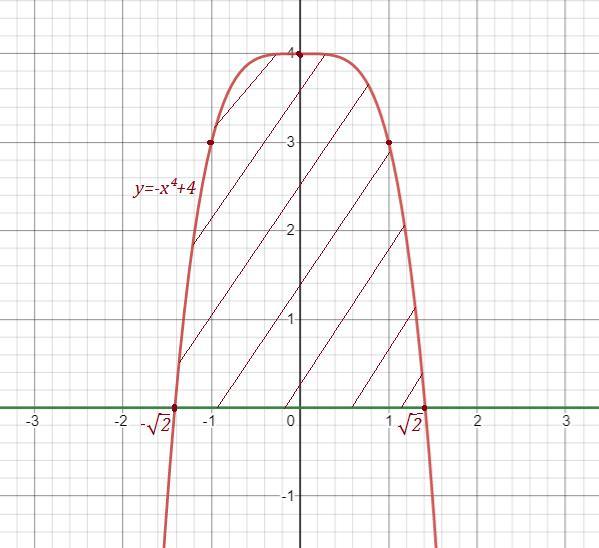
10. Найдите площадь фигуры ограниченной линиями: у =-x⁴+4; у = 0
Ответы
Автор ответа:
1
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: АружанИскакова
Предмет: Английский язык,
автор: SOvOeOtOa2001
Предмет: Русский язык,
автор: Graveti
Предмет: Информатика,
автор: diana1512041