Question

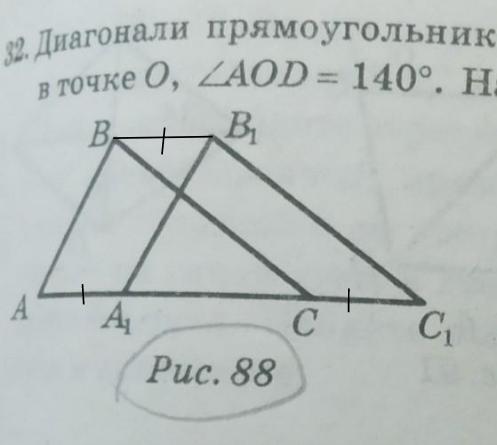
На рисунке 88 АВ=А1В1 ВС=В1С1 АС=А1С1. Найдите отрезок А1С, если ВВ1=8 см АС1=18 см​ СРОЧНО ПРОШУ​ номер 31

Answer 1

Ответ:

А1С=2см

Объяснение:

∆АВС=∆А1В1С1, по трем сторонам.

АС- общая часть.

ВВ1- общая сторона двух параллелограмов. ВВ1С1С и ВВ1А1А

ВВ1=СС1

ВВ1=АА1

А1С=АС1-2*ВВ1=18-2*8=18-16=2см

Answer 2

Ответ:

А1С=2 см

Объяснение:

Т.к по условию нам даны равные стороны, то треугольники АВС и А1В1С1 равны. Соединим В и В1. Образуется два параллелограмма АВВ1А1 и СВВ1С1.

Т.к это параллелограммы с общей стороной ВВ1, то АА1=СС1=ВВ1=8 см. Получается, что АС1=АА1+А1С+СС1=8+А1С+8=16+А1С. Т.к АС1=18 см, то:

16+А1С=18 Получаем, что А1С=2 см (Это не точно, но к моему мнению стоит присмотреться)