Question

найдите объём правильной шестиугольной пирамиды, высота которой равна √3 см а боковое ребро составляет 2 см​

Answer 1

Объяснение:

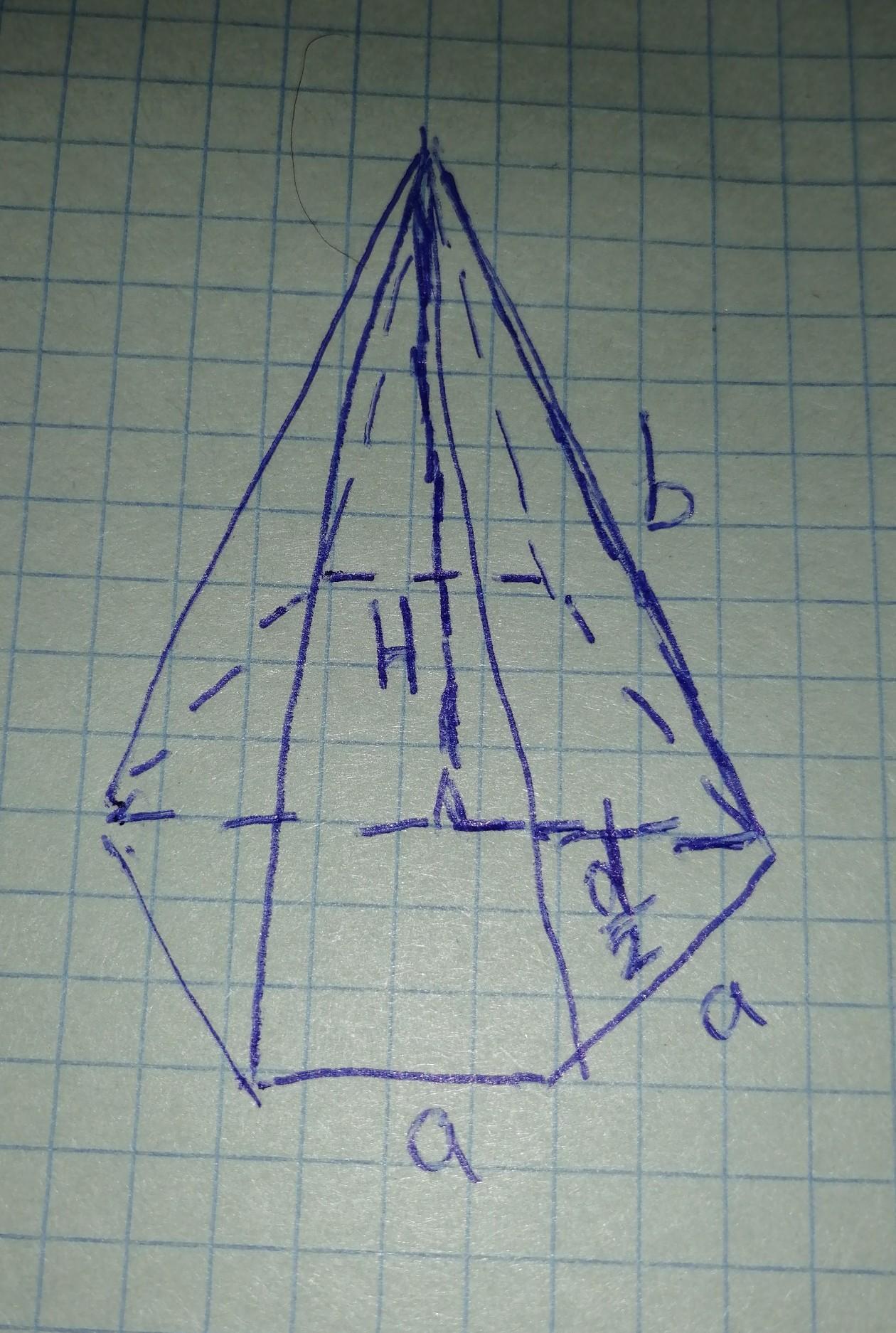
Правильная 6-ти угольная пирамида

Н=корень3 (см)

b=2 cм

Найти : V

Решение :

V=S×H /3

S-площадь основания

S=(3×a^2×корень3) /2

а-ребро основания

По теореме Пифагора :

d-диагональ основания

d/2=корень(b^2-H^2)=

=корень (2^2-(корень3) ^2)=

=корень (4-3)=1

d=1×2=2 cм

а=d/ 2=2/2=1 cм

S=(3×1^2×корень3) /2=3×1×корень3 /2=

=3/2×корень3

V=(3/2×корень3 ×корень3)/3 =

=(3×3/2)/3=9/2:3=9/2×1/3=3/2=1,5 см^3

Answer 2

Ответ:

V=1,5 см³

Объяснение:

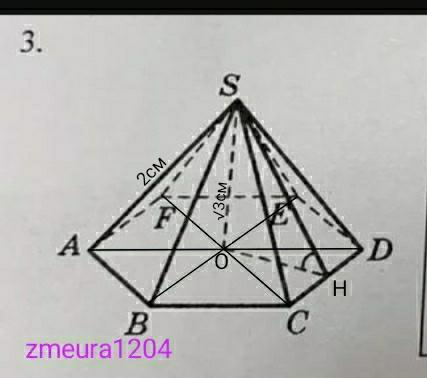
Теорема Пифагора

АО=√(SA²-SO²)=√(2²-(√3)²)=√(4-3)=1см.

Правильный шестиугольник делиться на 6 равносторонних треугольников.

Sосн=6*АВ²√3/4=6*1²√3/4=1,5√3 см²

V=1/3*Sосн*SO=1/3*1,5√3*√3=1,5 см³