Предмет: Геометрия,
автор: eaveranov98
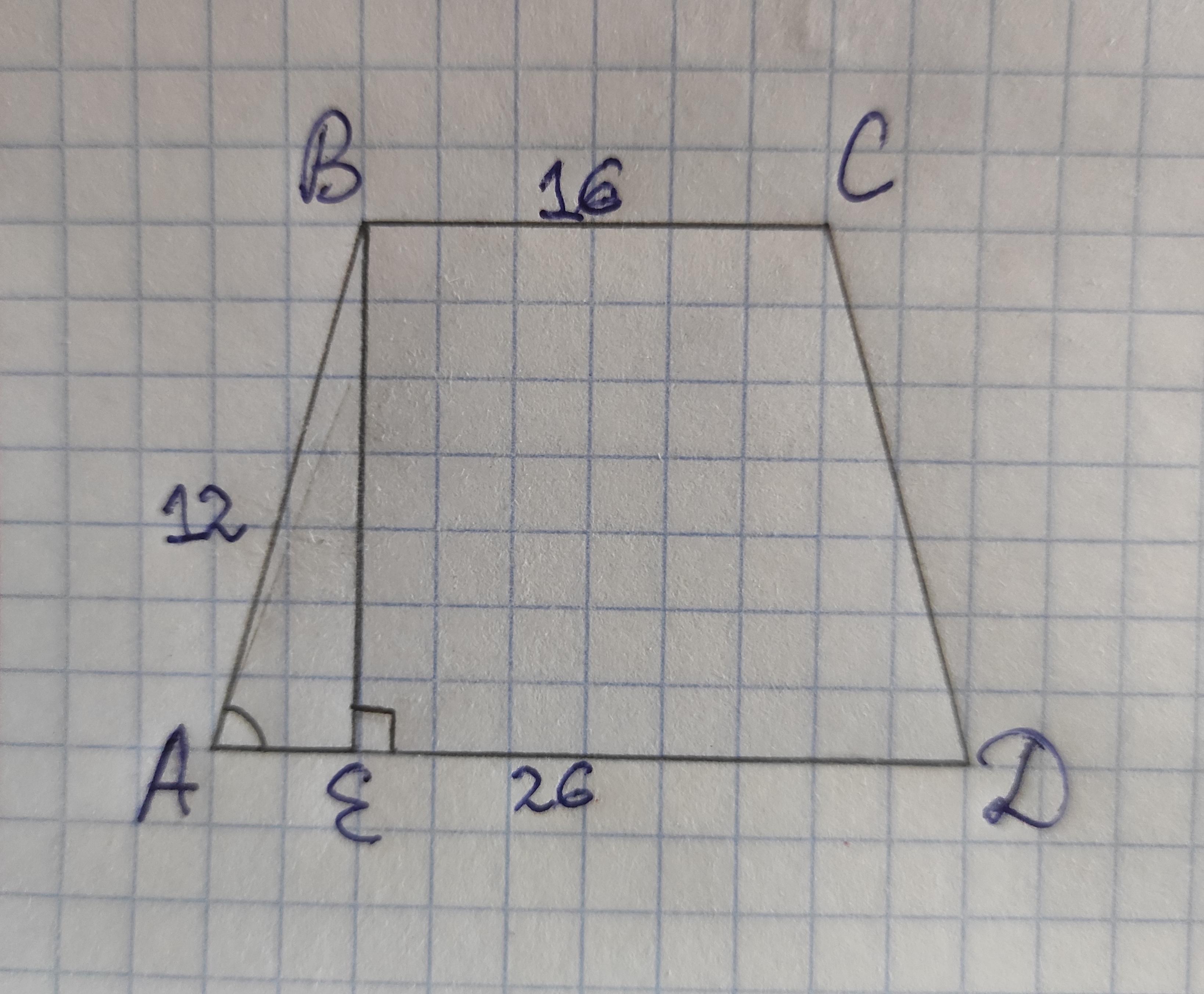
В равнобедренной трапеции с основаниями 16 и 26 см - боковая сторона равна 12 см. Найдите синус острого угла трапеции.
Ответы
Автор ответа:
0
Ответ:
√119 / 12
Объяснение:
Дано:
ABCD — трапеция, AB = CD
BC = 16 см, AD = 26 см, AB = 12 см
Найти: sin ∠A
1) Воспользуемся свойством равнобедренной трапеции: высота, проведенная с вершины тупого угла, делит большее основание на два отрезка, меньший из которых равен полуразности оснований.
ABCD — трапеция, AB = CD, BE ⊥ AD ⇒ AE = (AD-BC) / 2 = (26-16) / 2 = 5 (см)
2) ΔAEB — прямоугольный (∠AEB = 90°) ⇒ по теореме Пифагора
sin ∠A = BE / AB = √119 / 12
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: leeroi
Предмет: Английский язык,
автор: врала558
Предмет: Беларуская мова,
автор: оля593
Предмет: Русский язык,
автор: простэйшион
Предмет: Математика,
автор: kakakakkakakak6