Предмет: Математика,
автор: VladimirRosipov
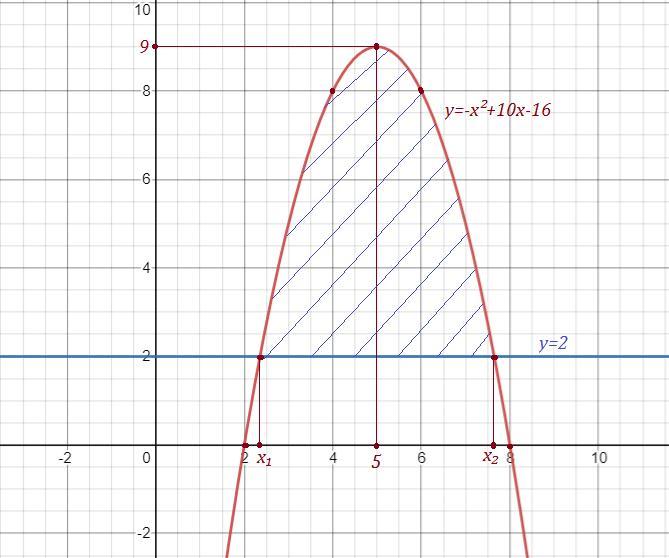
Найти площадь фигуры, ограниченной линиями
Y=-x^2+10x-16, y=2
ildar502020:
пределы интегрирования дробные???
проверьте условие
Такое задание
Я в прямом смысле ничего не понимаю в этом задании, поэтому мне нужно полное решение
Ответы
Автор ответа:
1
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: MarwinPro
Предмет: Другие предметы,
автор: эльза555552
Предмет: Русский язык,
автор: Кисазая111
Предмет: Математика,
автор: Yanabanana11