Предмет: Математика,
автор: zXvXz
Помогите пожалуйста с математикой, срочно нужно!!!
Приложения:
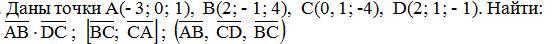
LymarIvan:
это скалярное, векторное и смешанное произведения?
да
Ответы
Автор ответа:
2
Ответ:
-19
(2; 34; 8)
-28
Пошаговое объяснение:
Координаты вектора найдем, отняв от координат его конца соответствующие координаты начала.
Скалярное произведение векторов в базисе {i; j; k} равно сумме произведений их соответствующих координат:
Векторное произведение векторов найдем, вычислив такой определитель:
Смешанное произведение векторов найдем, вычислив определитель, в котором строки — эти векторы, представленные координатами:
Спасибо огромное))
Похожие вопросы
Предмет: Русский язык,
автор: Uclam
Предмет: Русский язык,
автор: ильинавика
Предмет: Английский язык,
автор: pluha410
Предмет: Обществознание,
автор: asokoreva
Предмет: Биология,
автор: gerfes