Предмет: Алгебра,
автор: 1488Vadik777
Помогите пожалуйста, задание с определенным интегралом
Приложения:
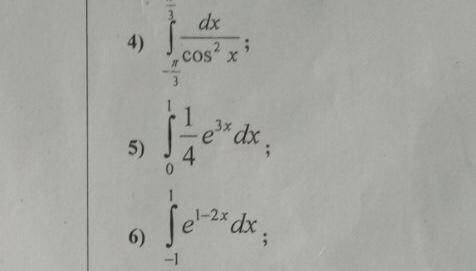
Ответы
Автор ответа:
1
Ответ:
4) 2√3
5) (e³-1) / 12
6) (e³-e^-1) / 2
Объяснение:
4)
5)
6)
Похожие вопросы
Предмет: Русский язык,
автор: ШЕЛЧОК
Предмет: Русский язык,
автор: алишер45
Предмет: Русский язык,
автор: Markiza12
Предмет: Математика,
автор: якудзи
Предмет: Математика,
автор: antoxa5767