помогите пожалуйста.....

Ответы
Ответ:
(куб. ед.)
Пошаговое объяснение:
(1)
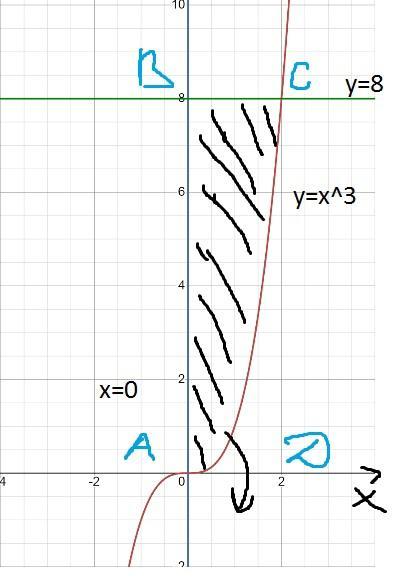
Найдём значение аргумента x функции при y=8, учитывая то, что слева тело ограничено x=0:
,
Т.е. тело, полученное вращением фигуры, ограниченной (1), ограничено слева: x=0; справа: x=2; сверху: y=8; и, т.к. вращение вокруг оси ОХ, снизу: y=-8.
Вычислим объём полученного тела следующим образом:
Из объёма цилиндра, полученного вращением прямоугольника ABCD вокруг оси OX вычтем объём фигуры, ограниченной линиями (2), рис.2
Вычислим объём цилиндра. Радиус основания равен AB=R=8; высота равна CD=H=2.
(3)
Объём фигуры, ограниченной линиями (2), вычислим по формуле:
Подставляем:
(4)
Итак, чтобы получить объём тела полученного вращением фигуры, ограниченной линиями (1), осталось из объёма цилиндра (3) отнять объём фигуры (4):
(куб. ед.)