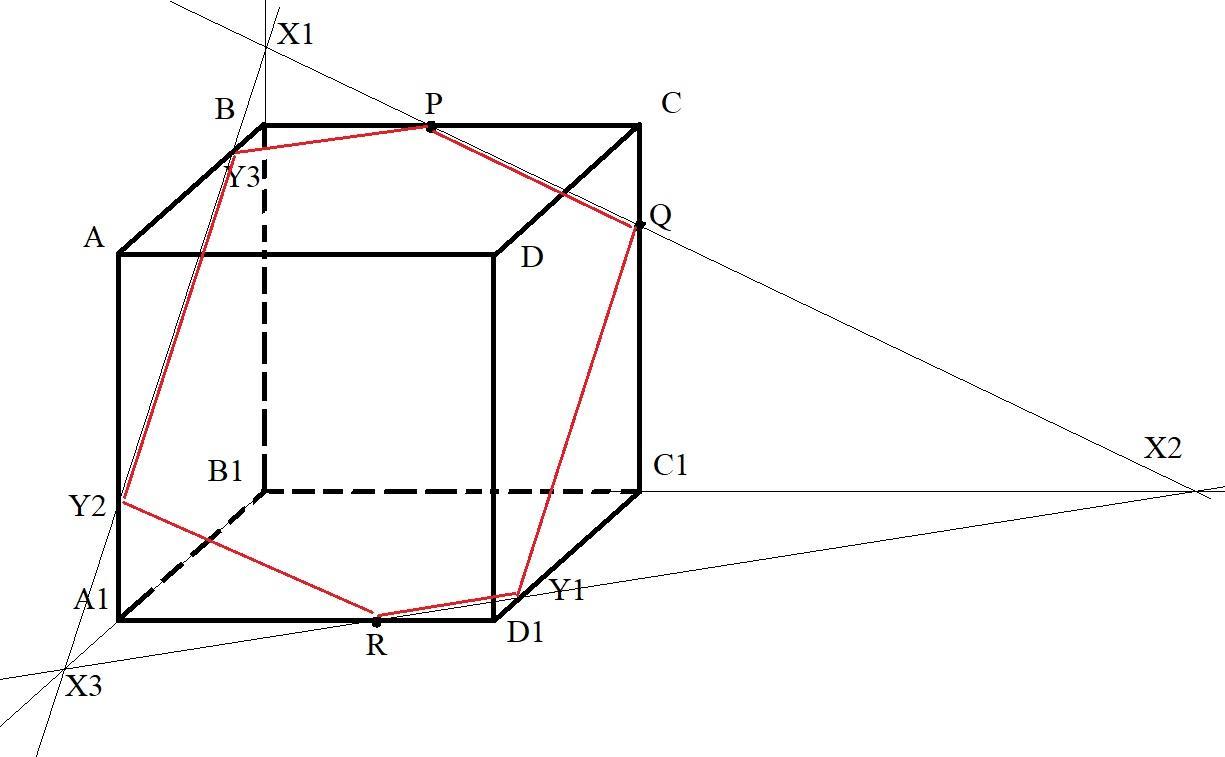
Точка P - середина ребра BC куба ABCDA1B1C1D1. Точки Q и R расположены на ребрах cc1 и a1d1 так, что CQ:QC1 = 1:3 , A1R:RD1 = 4:1. Построить сечение плоскостью PQR и найти отношения, в которых оно делит пересекаемые ребра. Может кто-нибудь помочь?
Ответы
Ответ:
Остальные ребра разделятся сечением в отношении 2/15; 3/2; 12/5
Пошаговое объяснение:
Построение сечения.
В основе построения сечения куба лежит принцип - прямая пересекающая два ребра куба пересекает и прямые на которых лежат другие два ребра этого куба.
См. чертеж.
1) Проведем прямые:
через точки В и В1
через точки В1 и С1
через точки P и Q
Так как все эти точки лежат в плоскости грани ВСС1В1, то точки пересечения построенных прямых тоже лежат в этой плоскости.
Обозначим пересечение прямых ВВ1 и PQ точкой Х1
Обозначим пересечение прямых В1С1 и PQ точкой Х2
Прямая Х1Х2 лежит и в плоскости грани ВСС1В1 и в плоскости сечения PQR.
2) Точка Х2 лежит в грани A1B1C1D1 так как лежит на ребре B1C1
Точка R лежит в плоскости сечения PQR.
Следовательно грань A1B1C1D1 и сечение PQR пересекаются по прямой Х2R.
Следовательно прямая Х2R пересекает и ребро A1B1.
Проведем прямую A1B1 и получим точку Х3 - точку пересечения прямой Х2R и прямой A1B1.
Кроме того прямая Х2R пересекает и ребро C1D1. Обозначим точку их пересечения Y1.
3) Точка Х3 лежит в грани ABB1A1 так как лежит на ребре A1B1
Точка Х1 лежит в плоскости сечения PQR (см п.1).
Следовательно грань ABB1A1 и сечение PQR пересекаются по прямой Х3Х2.
Следовательно прямая Х3Х2 пересекает и ребра AA1 и AB
Обозначим эти точки пересечения Y2 и Y3 соответственно.
Шестиугольник PQY1RY2Y3 - искомое сечение.
Вычислим отношения, в которых сечение делит пересекаемые ребра.
Пусть ребро куба равно 1 тогда
PC = PB = 0,5
CQ = 0,25
QC1= 0,75
RD1 = 0,2
RA1 = 0,8
Треугольники PBХ1 и PCQ подобны. Тогда X1B = 0,25
Треугольники PC1Q и X2C1Q подобны. Тогда C1X2 = 1,5
Треугольники Y1C1X2 и Y1D1R подобны. Тогда Y1D1 = 2/17 и Y1C1 = 15/17
Треугольники Y1D1R и X3A1R подобны. Тогда X3A1 = 8/17
Треугольники X3Y2A1 и X3X1B1 подобны. Тогда Y2A1 = 0,4 и Y2A = 0.6
Треугольники X3A1Y2 и Y3AY2 подобны. Тогда AY3 = 12/17 и Y3B = 5/17
Следовательно ребро D1C1 делится точкой Y1 в отношении
D1Y1/Y1C1 = (2/17)/(15/17) = 2/15
Следовательно ребро AA1 делится точкой Y2 в отношении
AY2/Y2A1 = 0,6/0,4 = 3/2
Следовательно ребро AB делится точкой Y3 в отношении
AY3/Y3B = (12/17)/(5/17) = 12/5