Question

исследовать функцию на экстремум построить график функции по пунктам y= -3x^2-6x-1​

Answer 1

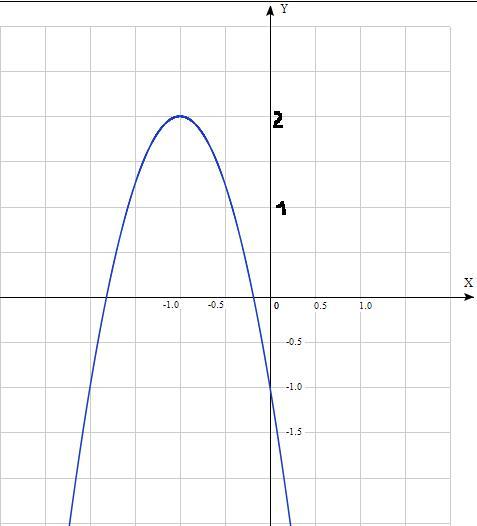
y= -3x²-6x-1​ сразу видно что это парабола , ветви вниз , верштна х₀=6:(-6)= -1 , у₀=-3+6-1=2

1)Область определения D(y) ∈(-∞ ;+∞)

2)область допустимых значений E(y) ∈(-∞ ;+∞)

3)Четность, нечетность функции  y(х)= -3x²-6x-1​ .

y(-х)= -3(-x)²-6*(-x)-1​=  -3x²+6x-1​ ≠ у(х)≠ -у(х) общий вид

4)Точки пересечения с осями.

С оу , х=0 , y(0)= -3*0²-6*0-1​ = -1

С ох , у=0 ,  -3x²-6x-1​=0,    3x²+ 6x +1​=0 ,    D=36-12=23=4*6

х₁= (-6-2√6):6≈1,8       х₂=  (-6+2√6):6≈-0,2

5)Экстремумы Точки перегиба

y'(х)=( -3x²-6x-1​ )'=-6x-6= -6(x+1)

-6(x+1) =0 ,x=-1

    +                            -

_________(-1)_______

возр          макс    убывает

у(-1) = -3+6-1=2

x=-1 т перегиба

Answer 2

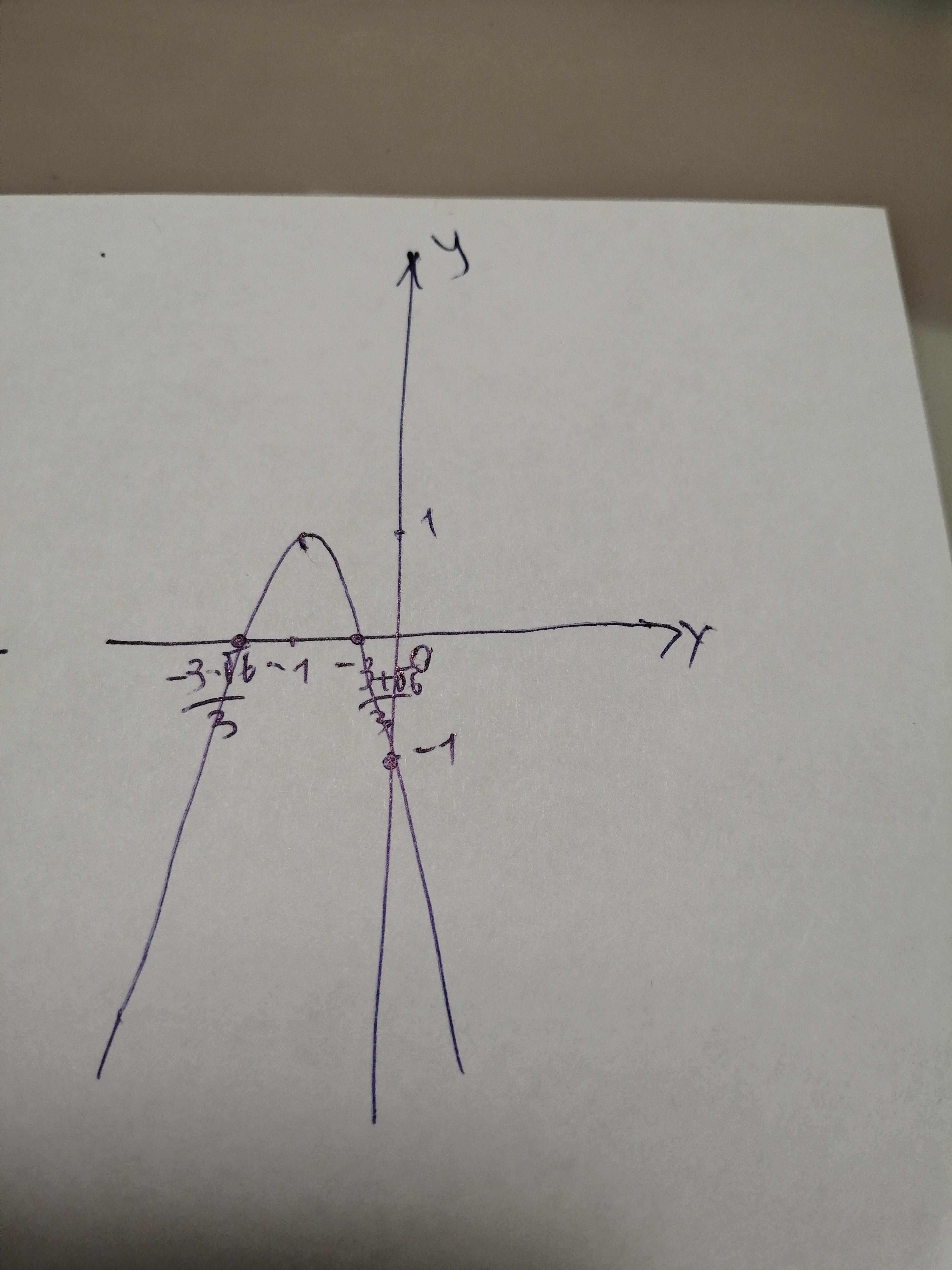
Ответ:

Пошаговое объяснение:

Всё подробно написала в решении.