ПОМОГИТЕ ПОЖАЛУЙСТА
Радианное измерение углов и дуг. Соотношения между градусной и радианной мерами угла. Тригонометрические функции числового аргумента. Знаки их значений. Соотношения между тригонометрическими функциями одного аргумента
Ответы
Ответ:
Ответ в объяснении
Пошаговое объяснение:
Радианы - ещё одна единица измерения углов помимо градусов. 1 радиан равен примерно 57 градусам. Радианы не имеют специального знака в отличие от градусов (°). Обычно углы в радианах содержат в себе число пи (π). Оно получается из отношения длины окружности к её диаметру.
π=180°, отсюда можем значение любого угла в градусах выразить в радианах: если нужно перевести угол из градусов в радианы, умножаем имеющееся значение на π/180, если из радиан в градусы, эту дробь переворачиваем, т.е. умножаем на 180/π.
Тригонометрическая функция от числа выглядит так: sin(k), cos(k), tg(k), ctg(k), где k - какое-то число. Важно учитывать, что аргументы (число k) синуса и косинуса могут варьироваться в пределах от -1 до 1 включительно. Если k выходит за эти пределы, то такой синус или косинус найти нельзя.
Теперь немного про чётность этих функций. Чётность, проще говоря, это симметричность графика функции, т.е. если график функции можно "сложить пополам" так, чтобы линия сгиба была на оси ординат (она же ось y), и при этом одна часть графика наложится на другую, можно говорить о том, что функция чётная. Если посмотреть на графики всех тригонометрических функций, станет понятно, что чётная из них только y=cos(x) (графики прикрепляю). В чём эта чётность выражается на практике? В том, что, если мы решаем какое-то уравнение, например, с синусом (возьмём для примера sinx=π/6), то корни этого уравнения выглядят следующим образом: x = arcsinα+2πn x=π-arcsinα+2πn, n ∈ Z (в нашем случае x = arcsin(π/6)+2πn x=arcsin(π-π/6)+2πn, n ∈ Z). С косинусом всё немного проще: хоть там тоже получается два корня, их можно записать в общем виде как +-arccosα+2πn, n ∈ Z. Вот что представляет из себя чётность функции, если записать её в алгебраическом виде: cos(x)=cos(-x), т.е. функция от аргумента равна функции этого же аргумента с противоположным знаком. (с синусом, тангенсом и котангенсом это не работает: sinx≠sin(-x), tgx≠tg(-x), ctgx≠ctg(-x)). Можно проверить, подставив любые табличные значения.
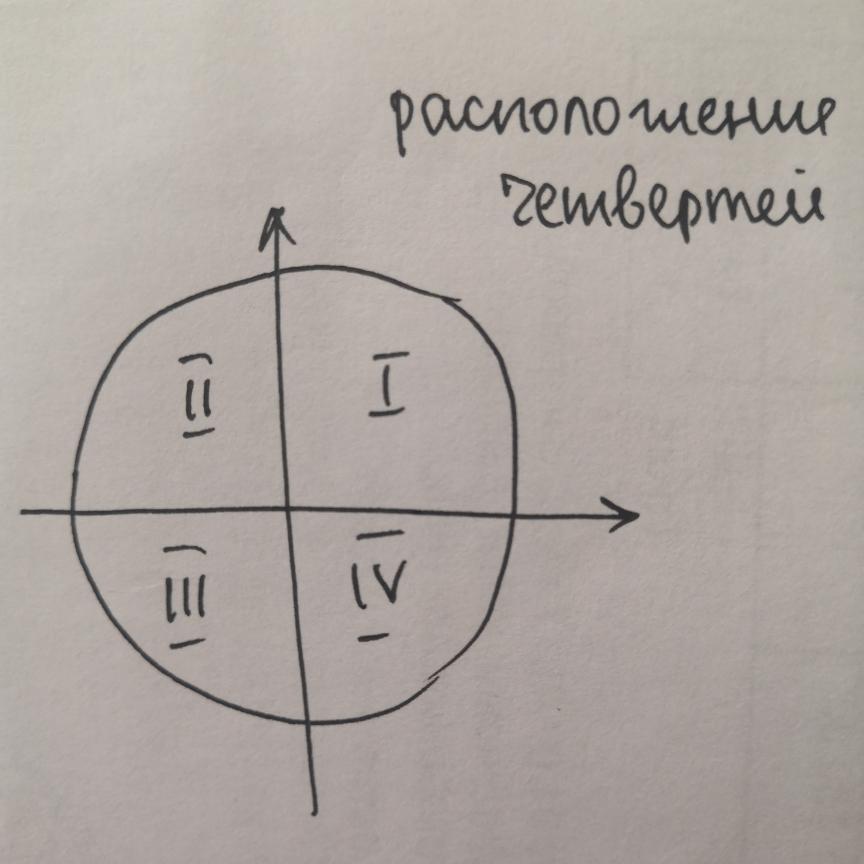
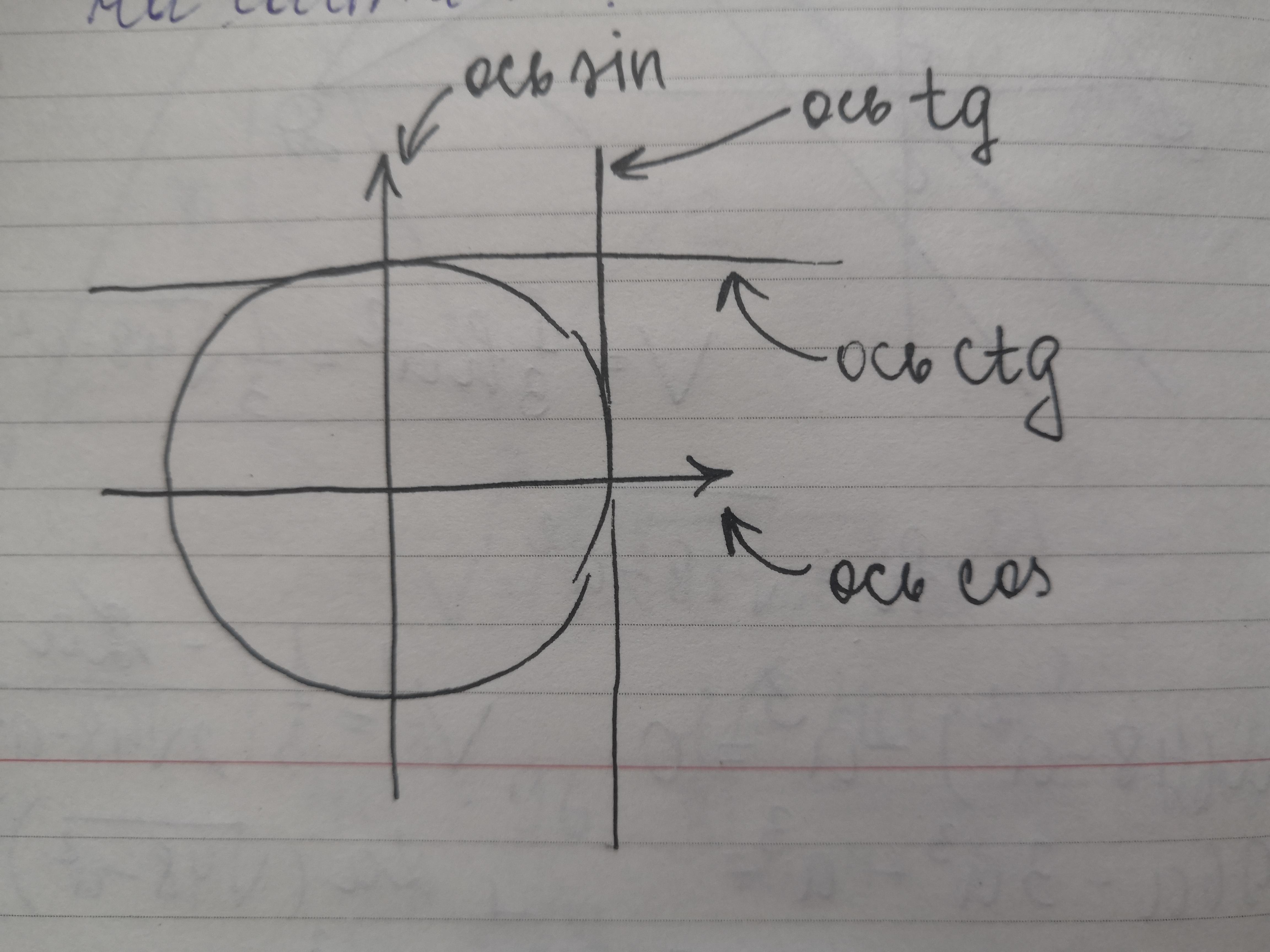
Теперь про знаки тригофункций на координатной плоскости. Начать стоит с определения того, какие оси каким функциям соответствуют. Ось абсцисс (ось х) - это ось косинусов, ось ординат (ось у) - ось синусов, вертикальная ось, проходящая через точку х=1, - ось тангенсов, горизонтальная ось, проходящая через точку у=1, - ось котангенсов. Понятнее станет, если посмотрите на картинку. Кроме того, существуют так называемые четверти: это области на координатной плоскости. Они обозначаются римскими цифрами от I до IV. На фото покажу, как они располагаются. А теперь представим эти оси и четверти на одном рисунке. Получится, что ось синусов выше 0, т.е. положительна в I и II четвертях, а отрицательна, соответственно, в III и IV, ось косинусов положительна в I и IV четвертях, а отрицательна - в II и III, тангенс и котангенс имеют знак + в 1 и 3 четвертях, отрицательны они в 2 и 4 (это получаем из tg=sin/cos=1/ctg). Если сложно, лучше просто выучить знаки в четвертях (приложу фото).
Теперь про соотношения между тригофункциями одного аргумента. Частично это объяснялось в абзаце про чётность, но объясню ещё раз. При решении тригоуравнений в общем виде корни выглядят так:
(r - это просто какое-то число)
sinx=r
x=arcsinr+2πn, n ∈ Z или x=arcsin(π-r)+2πn, n ∈ Z ("или" не значит, что можно записывать что-то одно, оба корня должны быть, их можно не только записать через "или", но и объединить знаком совокупности (не фигурная скобка!!!! квадратная!!))
cosx=r
x=+- arccosr+2πn, n ∈ Z
tgx=r
x=arctgr+πn, n ∈ Z (здесь и в котангенсе через период πn объединены два корня, т.е. изначально их было 2 и у каждого был период 2πn, но можно записывать один через πn)
ctgx=r
x=arcctgr+πn, n ∈ Z
Фух, кажется, всё! Если есть вопросы, задавайте. Могу ещё объяснить способ нахождения тригофункций табличных углов без запоминания таблицы и то, как пользоваться формулами приведения, не запоминая их :3