Предмет: Математика,
автор: glebigrovoy
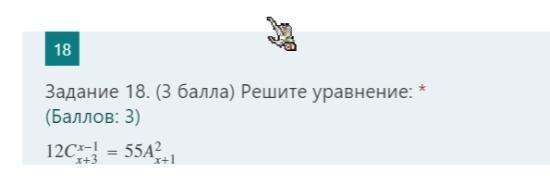
решите уравнение
очень нужно,срочно
Приложения:
Ответы
Автор ответа:
0
Ответ:
8
Пошаговое объяснение:
По теореме Виета
при x = -13 комбинаторные конфигурации не определены, поскольку n и k должны быть неотрицательными
Похожие вопросы
Предмет: Английский язык,
автор: guldanasagitzhan
Предмет: Английский язык,
автор: nastyatolkotss
Предмет: Английский язык,
автор: Анастасияnasta
Предмет: Английский язык,
автор: elenayab
Предмет: Математика,
автор: Аноним