Помогите решить пожалуйста
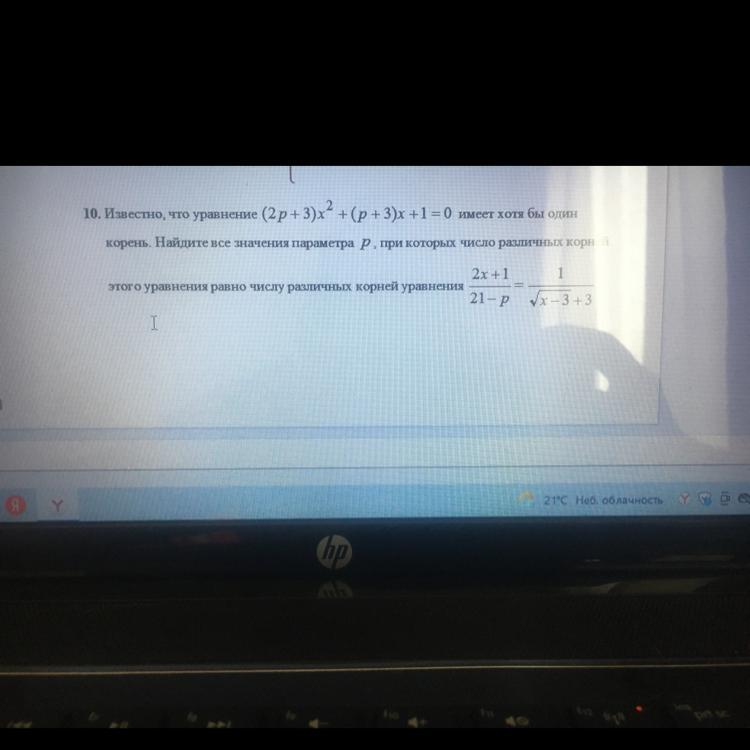
Ответы
Ответ:
-1,5; -1
Пошаговое объяснение:
Рассмотрим первое уравнение.
Если , то это линейное уравнение:
. При данном p уравнение имеет один корень.
Если , то это квадратное уравнение, количество его корней зависит от дискриминанта.
Уравнение имеет один корень при . Два различных корня — при
, за исключением значения p = -1,5.
Таким образом, уравнение имеет один корень при p = -1,5; -1; 3. Два различных корня — при p < 1, p > 3 и p ≠ -1,5.
Рассмотрим второе уравнение.
Справа представлена убывающая функция. Действительно, если взять , то
. Значит, максимальное значение функции достигается в точке x = 3 (поскольку она определена при x ≥ 3). При этом функция ограничена снизу нулём, так как все её значения положительны.
Слева представлена линейная функция с коэффициентом при x , график которой проходит через точку (-0,5; 0). Если коэффициент положительный, т. е. p < 21, левая часть возрастает, а правая — убывает. Тогда уравнение имеет максимум один корень, если линейная функция проходит ниже максимума функции правой части, то есть:
(переворачивать дробь можно, так как p < 21, т. е. 21 - p > 0).
Если коэффициент отрицательный, т. е. p > 21, то функция убывает. При x > 0 , но правая часть положительна при данных x. Значит, при p > 21 уравнение не имеет корней.
Таким образом, уравнение имеет максимум один корень при p < 0. Так как первое уравнение имеет один корень при p = -1,5; -1; 3, нам подходят только значения -1,5 и -1.