Предмет: Алгебра,
автор: demeter165165
Помогите пожалуйста срочно! АЛГЕБРА.
Приложения:
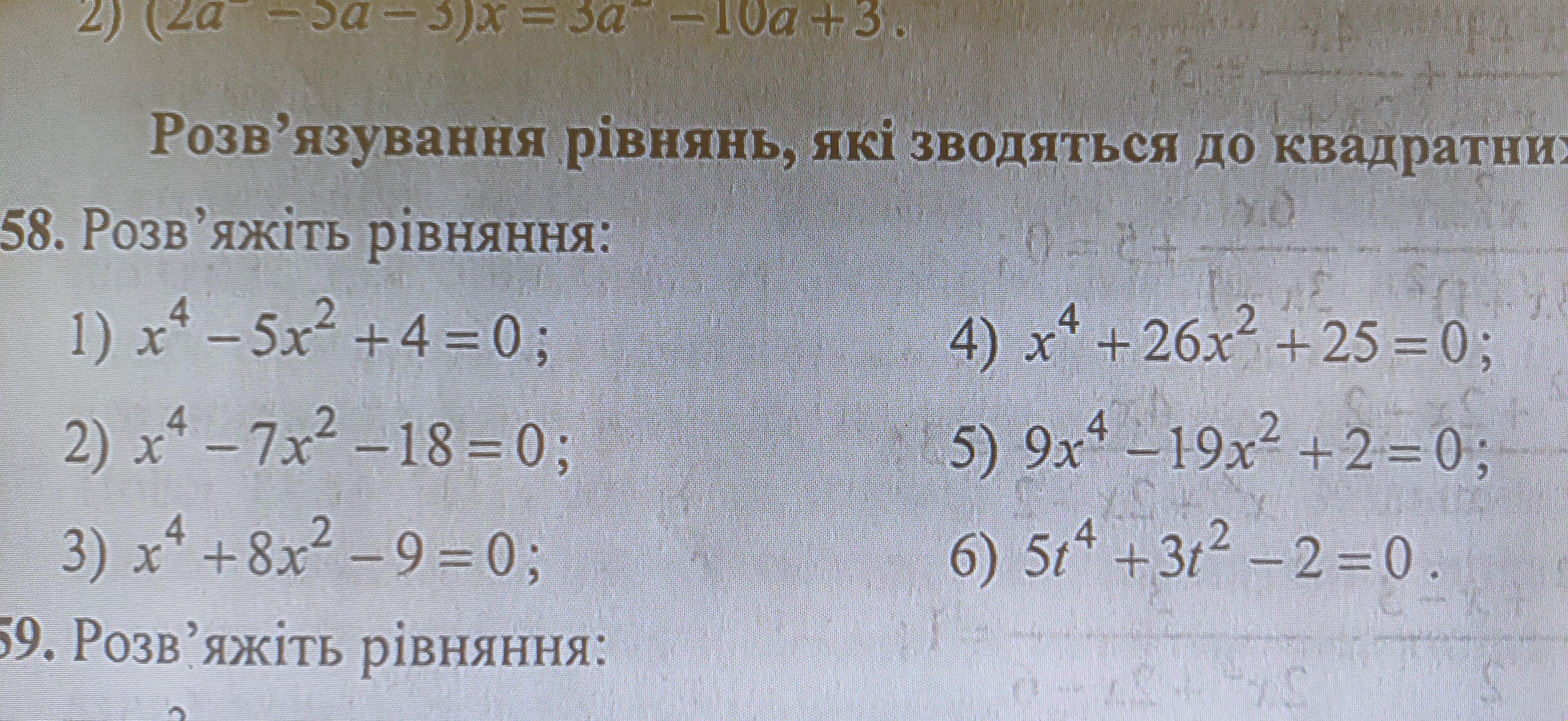
Ответы
Автор ответа:
2
Ответ:
Автор ответа:
3
Ответ:
Рівняння типу - це біквадратне рівняння і, щоб його розв'язати, треба
перетворити в
, потім треба скористатися методом внесення нової змінної, тобто
, тоді вийде звичайне квадратне рівняння
, знайошовши корені рівняння або через дискримінант, або через теорему Вієта, слід пам'ятати, що ми ж прирівнювали
, тому не треба поспішати записувати корені в відповідь, а наприклад, якщо
, то підставляємо:
- оце й буде відповіддю.
58. Розв'яжіть рівняння:
Похожие вопросы
Предмет: Русский язык,
автор: arina212
Предмет: Қазақ тiлi,
автор: карина484
Предмет: Русский язык,
автор: ярик103
Предмет: История,
автор: kirana05
Предмет: Русский язык,
автор: polinacat228