Предмет: Математика,
автор: niceguy0
Найти интеграл 60 баллов
Приложения:
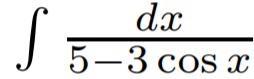
Ответы
Автор ответа:
0
Ответ: ∫ dx/(5 - 3cosx) = 1/8 * ln | tg²x/2 + 1/4 | + C .
Пошаговое объяснение:
Зробимо підстановку : tgx/2 = t , тоді х = 2arctgt ; dx =2dt/( 1 + t²) , a
cosx = ( 1 - t²)/( 1 + t²) . Підставляємо значення у даний інтеграл :
∫ dx/(5 - 3cosx) = ∫ [ 2dt/( 1 + t²)] / [5 - 3*(1 - t²)/( 1 + t²)] = ∫ 2dt/( 8t² + 2 ) =
= ∫ dt/ (4t² + 1 ) = 1/4 ∫ dt/ ( t² + 1/4 ) = 1/4 * 1/2 *ln | t² + 1/4 | + C =
= 1/8 * ln | tg²x/2 + 1/4 | + C .
Похожие вопросы
Предмет: Английский язык,
автор: LEONELMESSI1234
Предмет: Қазақ тiлi,
автор: klaraomarova50
Предмет: Қазақ тiлi,
автор: Анна3706027
Предмет: Русский язык,
автор: ТаняДорофеева
Предмет: Математика,
автор: LuCkY1111111111h