Уважаемые МОЗГи! Задание, достойное Вас!!
Найти общее решение линейного однородного уравнения с переменным коэффициентом.
Если можно, с подробным (пошаговым) решением.
Заранее спасибо))
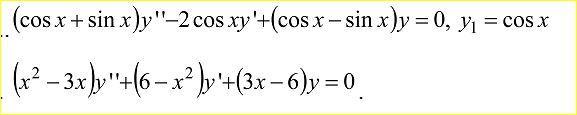
Ответы
Ответ:
1)
2)
Пошаговое объяснение:
ЛОДУ 2ого порядка с переменными коэффициентами имеет вид
Общее решение такого ДУ - линейная комбинация двух его линейно независимых частных решений.
В обоих заданиях необходимо заметить, что сумма коэффициентов равна 0. Значит, очевидно, одним из частных решений данного ДУ будет функция
[и действительно:
, а тогда уравнение принимает вид
- верное равенство].
1) Рассмотрим Вронскиан системы :
Значит, данные частные решения линейно независимы - а тогда общее решение имеет вид .
2) Очевидно искать частное решение в виде многочлена. Пусть его старший член равен [коэффициент при старшей степени не имеет значения, т.к. уравнение однородное], т.е.
.
Тогда
То есть коэффициент при старшей степени получаемого в левой части многочлена равен
[степень
не выше
, а
не выше
]. Но в правой части тождественный ноль - а значит если некий многочлен и является частным решением уравнения, то это многочлен степени 3.
Нетрудной подстановкой убеждаемся, что это решение ДУ:
- верное равенство.
А тогда общее решение имеет вид