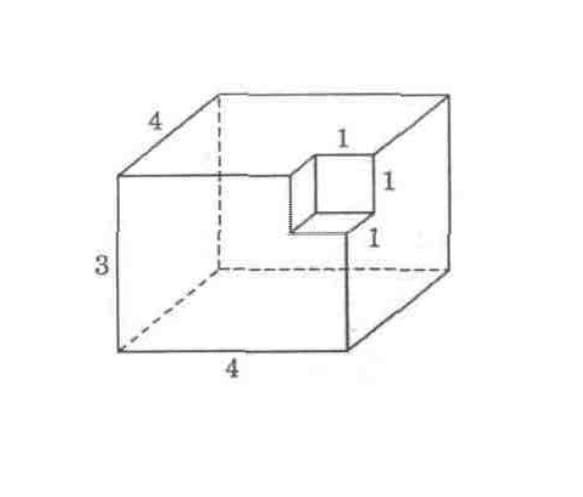
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы многогранника прямые). Помогите
Ответы
Ответ:
80
Объяснение:
Так как все двугранные углы прямые, то многогранник является прямоугольным параллелепипедом.
Первый способ решения
1) Площадь нижней грани:
4 · 4 = 16
2) Площадь верхней грани:
4 · 4 - 1 · 1 (вырез) = 16 - 1 = 15
3) Площадь боковой левой грани:
4 · 3 = 12
4) Площадь боковой правой грани:
4 · 3 - 1 · 1 (вырез) = 12 - 1 = 11
5) Площадь задней грани:
4 · 3 = 12
6) Площадь передней грани:
4 · 3 - 1 · 1 (вырез) = 12 - 1 = 11
7) Площади трёх плоскостей размером 1 х 1, находящихся в углублении:
1 · 1 · 3 = 3
8) ИТОГО: 16 + 15 + 12 + 11 + 12 + 11 + 3 = 80
Ответ: 80
Второй способ
Так как угловое углубление не меняет площади прямоугольного параллелепипеда, то её можно рассчитывать так, как если бы этого углового углубления не было.
4 · 3 · 2 ( передняя и задняя грани) + 4 · 3 · 2 (боковые грани) + 4 · 4 · 2 ( верхняя и нижняя грани) = 24 + 24 + 32 = 48 + 32 = 80
Ответ: 80