Предмет: Алгебра,
автор: anastasiaivanova2580
помогите пожалуйста очень срочно прошу вас умаляю
Приложения:
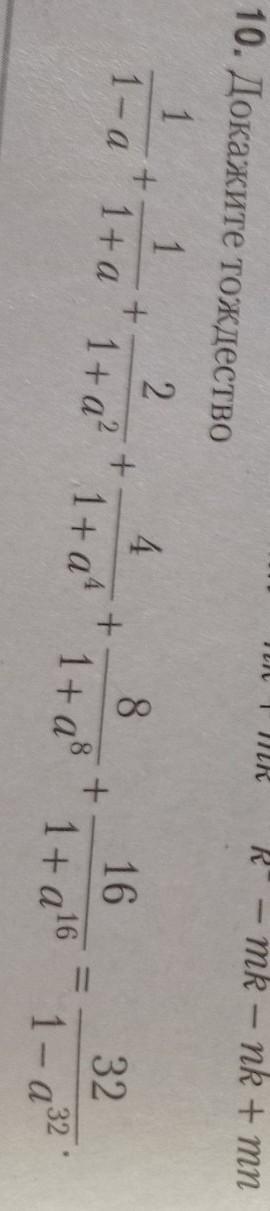
yugolovin:
УмОляю, а не умАляю
Ответы
Автор ответа:
0
Воспользуемся тождеством (проверяется непосредственно).
Имеем:
Похожие вопросы
Предмет: Русский язык,
автор: хорощист
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: нурай42
Предмет: Геометрия,
автор: greendan66rar