Предмет: Алгебра,
автор: 2001wlad1
решите предел пожайлуста
Приложения:
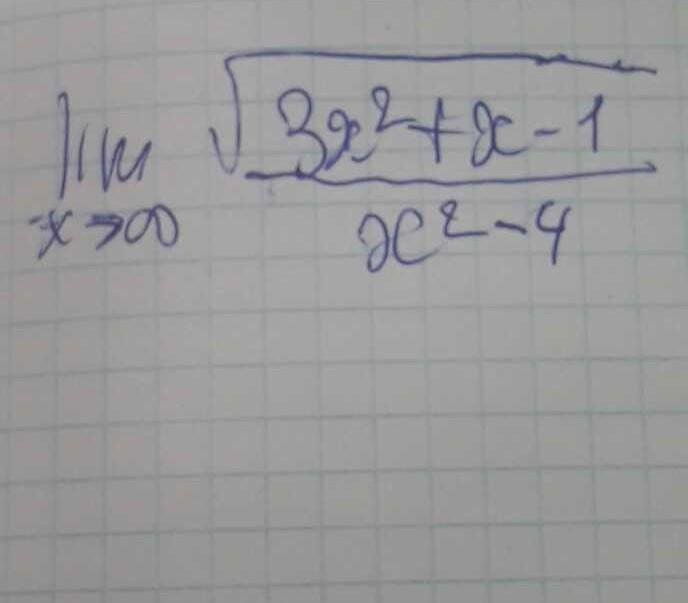
Ответы
Автор ответа:
1
Ответ: 0
Объяснение:
2001wlad1:
у меня красные циферки какие то
Почему 0 в конце?
Выражение в числителе стремится к нулю, в знаменателе - к единице. Ноль разделить на 1 - это ноль
Похожие вопросы
Предмет: Русский язык,
автор: ybakatovich
Предмет: Қазақ тiлi,
автор: йцук31
Предмет: Английский язык,
автор: агылшын
Предмет: Химия,
автор: Филиал4244