Предмет: Алгебра,
автор: astaxovvlad
Помогите пожалуйста Решить интеграл, очень срочно
Приложения:
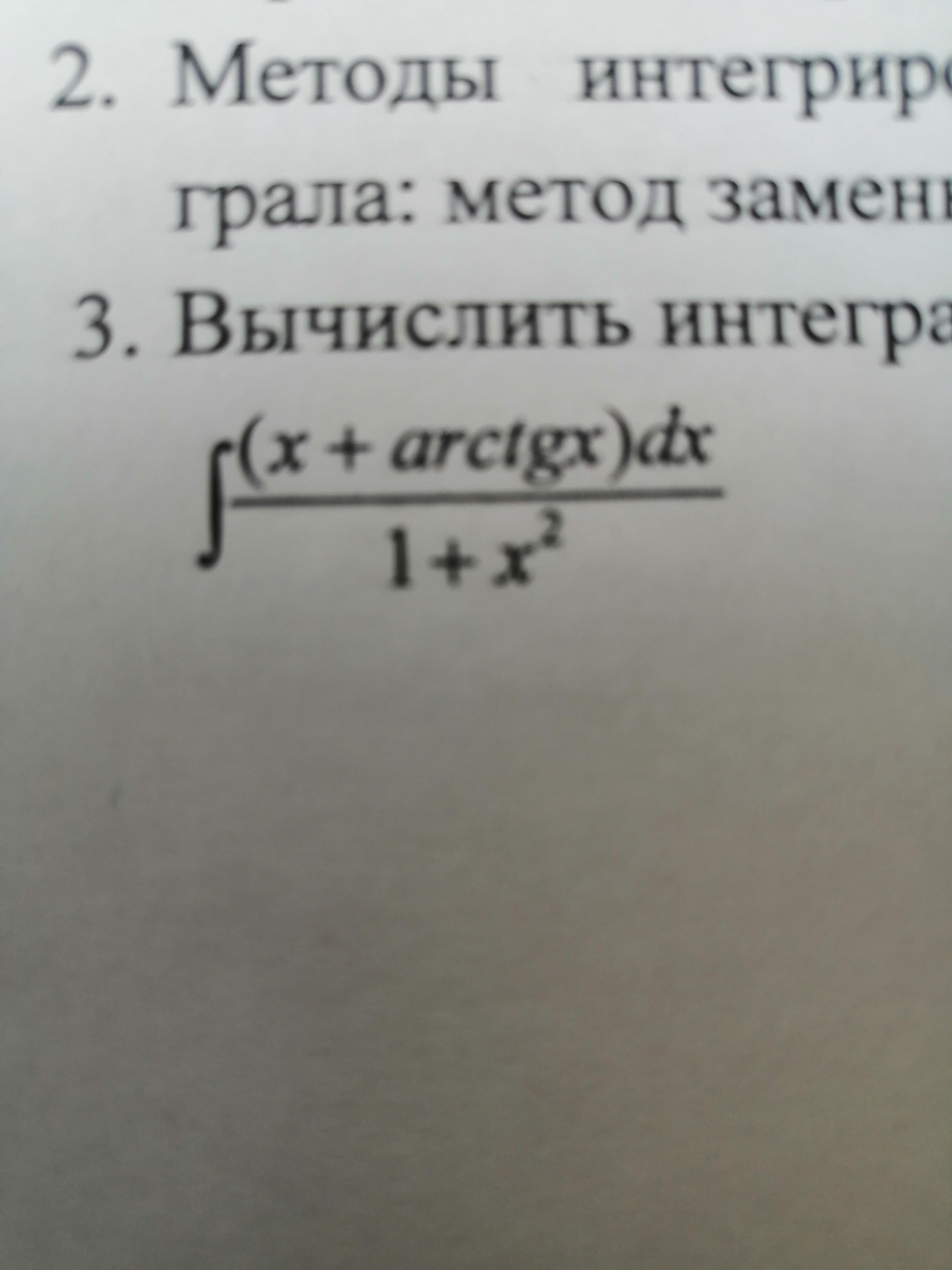
Ответы
Автор ответа:
0
Ответ:
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Evgsolnce
Предмет: Окружающий мир,
автор: kizelevf2016
Предмет: Русский язык,
автор: Сулейман111111
Предмет: Русский язык,
автор: FaKeJIoK
Предмет: Геометрия,
автор: pochivalovakari