Question

СРОЧНО помогите пожалуйста!! Найдите площадь четырехугльника, вершины которого имеют координаты (5:1), (7:4), (1:9), (5:8)

Answer 1

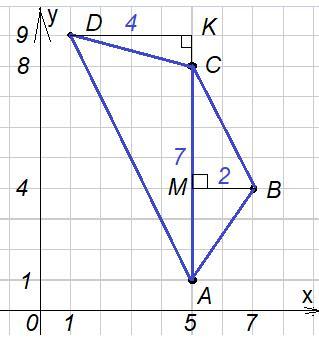
Построим на координатной плоскости заданные точки:

A(5;1),  B(7;4),  C(5;8),  D(1;9).

Проведём диагональ АС четырёхугольника ABCD.

$x_A=x_C=5;\ \ \ \Rightarrow\ \ \ AC=y_C-y_A=8-1=7$

Диагональ АС разбивает четырёхугольник ABCD на два треугольника: ACB  и  ACD, площади которых легко вычислить, пользуясь координатной плоскостью.

ΔACB   с основанием 7 и высотой 2:

$S_{\triangle ACB}=\dfrac 12\cdot AC\cdot BM=\dfrac 12\cdot 7\cdot 2=7$

ΔACD  с основанием 7 и высотой 4:

$S_{\triangle ACD}=\dfrac 12\cdot AC\cdot DK=\dfrac 12\cdot 7\cdot 4=14$

$S_{ABCD}=S_{\triangle ACB}+S_{\triangle ACD}=7+14=21$

Ответ: 21.