Предмет: Математика,
автор: alyabushevartem
общий интеграл дифференциального уравнения;
Приложения:
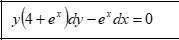
Ответы
Автор ответа:
0
Ответ:
общее решение
Похожие вопросы
Предмет: Русский язык,
автор: 752130
Предмет: Қазақ тiлi,
автор: Tatyana353
Предмет: Русский язык,
автор: mamankoka
Предмет: Русский язык,
автор: ulagajgold