Question

Решите пожалуйста задачу

Answer 1

Ответ:   723,7 ед².

Объяснение:

Решение.

S полная = 2S основания + S боковая.

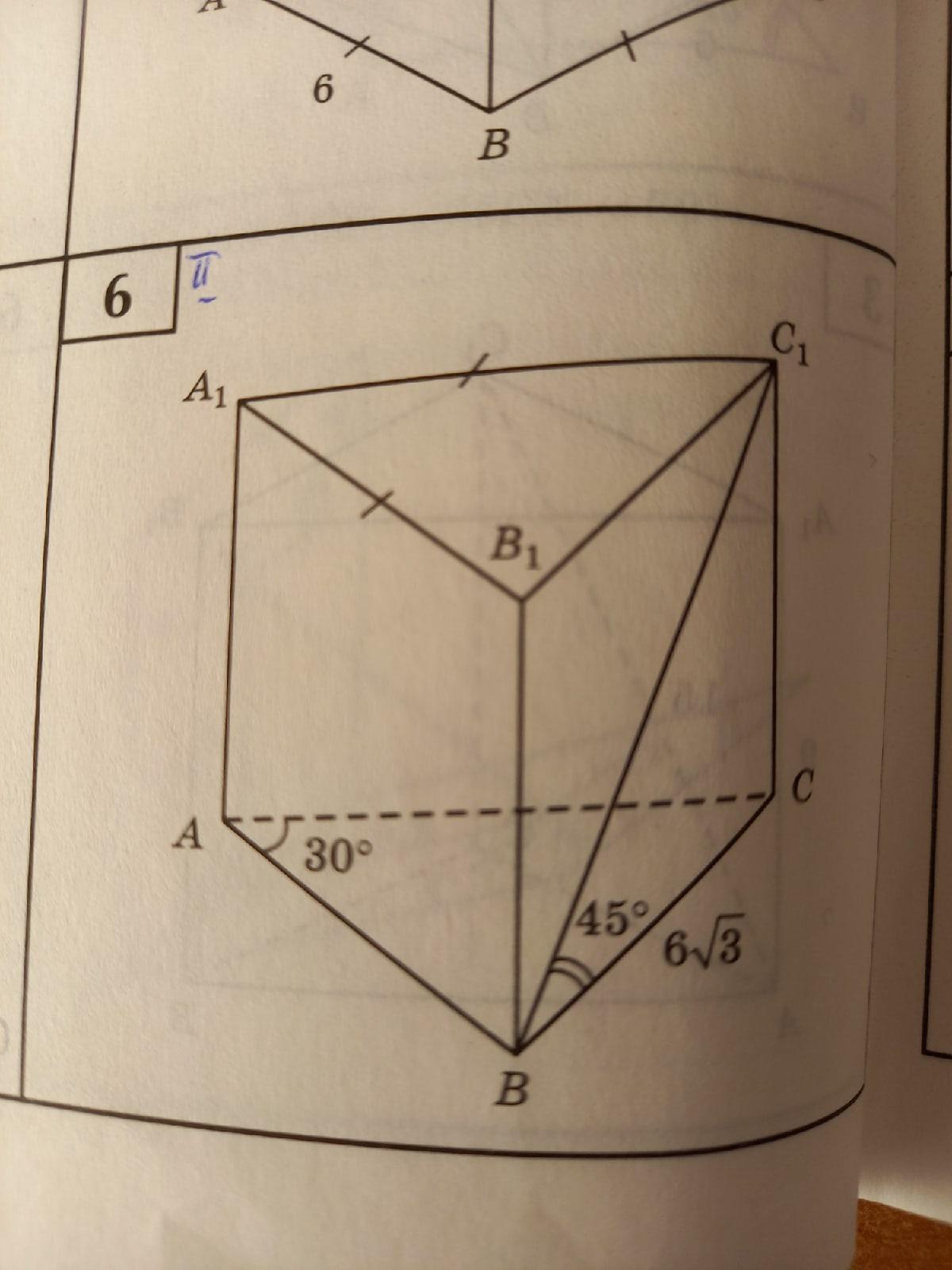
В основаниях лежит равнобедренный треугольник, основание которого равен 6√3 и углом при вершине 30°.

Пусть боковые стороны равны х, тогда по т. косинусов:

cosA=(b²+c²-a²)/2bc; так как b=с и a=6√3, а cos30=√3/2, то:

√3/2=2x²- (6√3)²/2x²;

2x²*√3/2=2x²- 108;

1.73x²-2x²=-108;

0.27x²=108;

x²=400;

x=20 см  - стороны основания.

Площадь основания равна

S основания=1/2(a*b*sin30°)=1/2(20*20*1/2)=100 см².

----------------

Площадь боковой поверхности S=P основания*Н, где

Р=(a+b+c)=20+20+6√3=40+6√3.

Так как угол С1ВС = 45°, то высота призмы Н=6√3.  Тогда  

S боковая = (40+6√3)*6√3 = 523,7.

------------

S полная =2*100+523.7=723,7 ед².