Предмет: Математика,
автор: alsulun1313
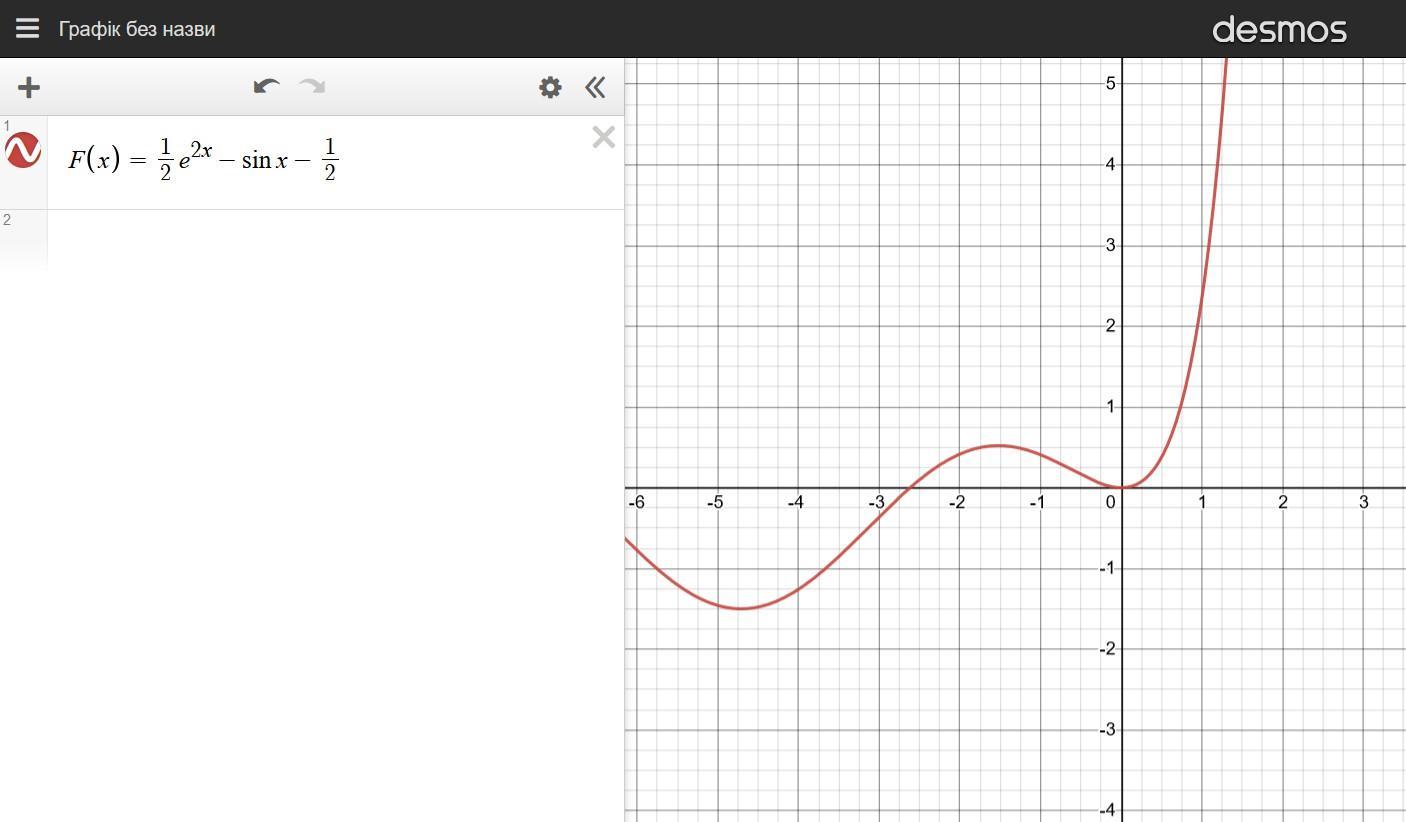
Найдите ту первообразную функции f(x)=e²ˣ-cos x, график которой проходит через начало координат
alsulun1313:
е в степени 2х
Ответы
Автор ответа:
2
Общий вид первообразных:
интегрируется как обычная показательная функция, если что:
Подставим в уравнение:
значения
и
, чтобы найти константу:
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: КРУТОЙ1337
Предмет: Английский язык,
автор: averry
Предмет: Окружающий мир,
автор: Arsenij34
Предмет: Русский язык,
автор: Volkovavika12
Предмет: Математика,
автор: СонливыйАнанас