Предмет: Математика,
автор: milakamilat1m
Помогите решить неопределенный интеграл, интегрирование по частям, пример:  . u=
. u= . Ответ должен быть:
. Ответ должен быть: 
Ответы
Автор ответа:
1
Ответ:
решение на фото........))))))..)
Приложения:
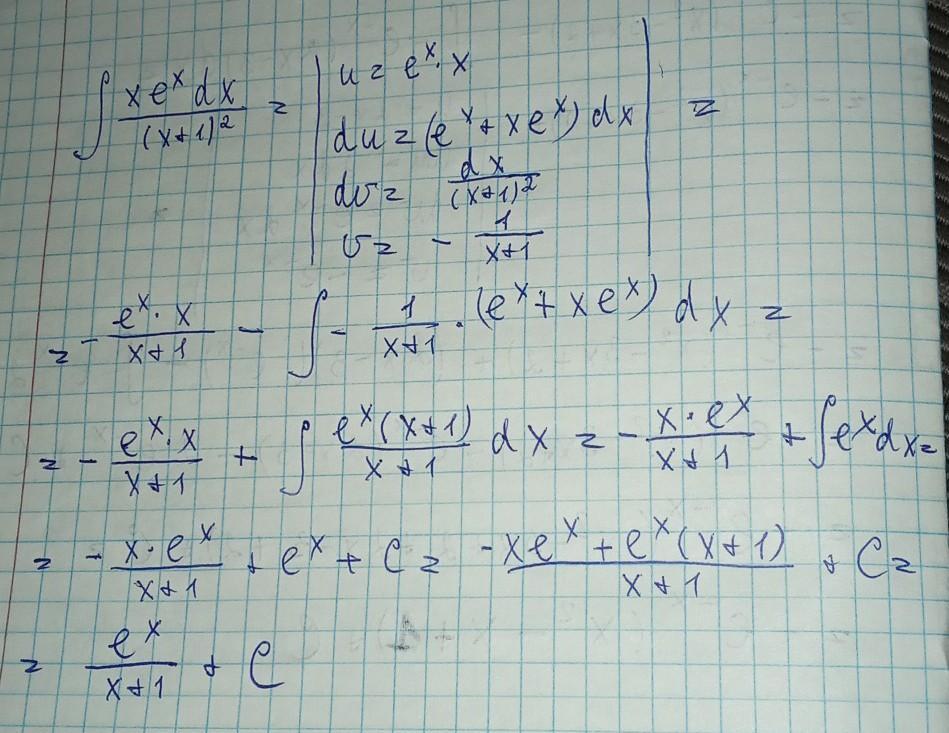
Автор ответа:
1
Ответ:
+C
Пошаговое объяснение:
=
[u=x du=
(1+x)dx dv=
v= -
]
= - +
=-
+
+C=
+C=
+C
Похожие вопросы
Предмет: Українська література,
автор: wwwdasha2
Предмет: Окружающий мир,
автор: лана102
Предмет: Русский язык,
автор: 5513076
Предмет: Физика,
автор: icecream21
Предмет: Русский язык,
автор: ГапоненкоДанил