Предмет: Математика,
автор: hman45656
Помогите решить систему уравнений. Пожалуйста даю 40 баллов.
Приложения:
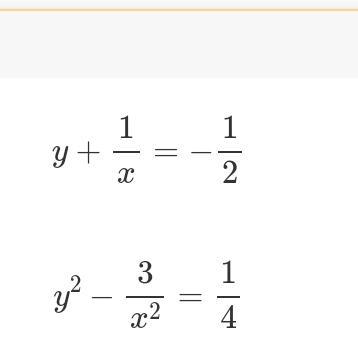
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
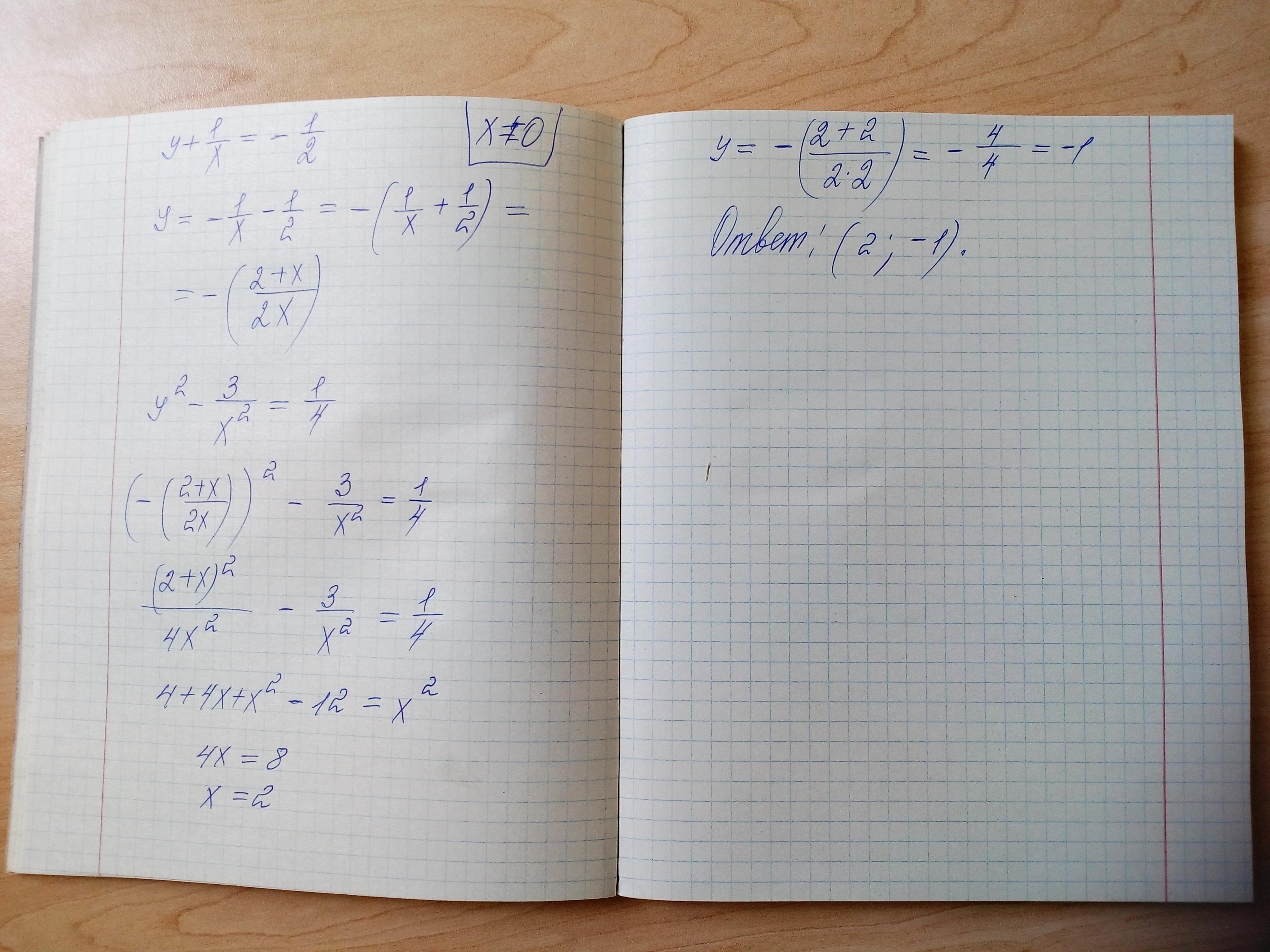
Автор ответа:
0
Ответ:
(2; -1)
Пошаговое объяснение:
Возведём второе уравнение в квадрат:
Правые части полученного уравнения и второго уравнения исходной системы равны, значит, левые тоже равны:
Подставим y в первое уравнение:
Решением будет пара (2; -1)
Похожие вопросы
Предмет: Русский язык,
автор: danruskaz
Предмет: Другие предметы,
автор: katynynka64
Предмет: Русский язык,
автор: настя2270
Предмет: Геометрия,
автор: денис1222