Question

Найдите область определения функции:
z(x,y)=√4-x²-y² ㏑(x²+y²-1)

Answer 1

Ответ:

$z(x,y)=\sqrt{4-x^2-y^2}\cdot ln(x^2+y^2-1)\\\\OOF:\ \left\{\begin{array}{l}4-x^2-y^2\geq 0\\x^2+y^2-1>0\end{array}\right\ \ \left\{\begin{array}{l}x^2+y^2\leq 4\\x^2+y^2>1\end{array}\right$

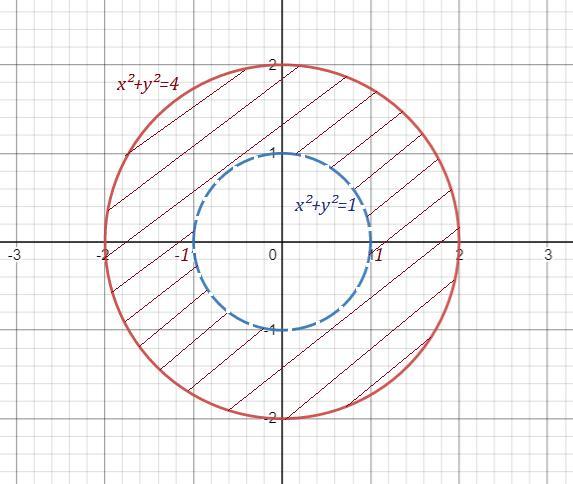
$x^2+y^2\leq 4$  -  это часть плоскости, лежащая внутри окружности с центром в точке (0;0) и радиусом  R=2 , граница круга входит в область .

$x^2+y^2>1$  -  это часть плоскости, лежащая вне окружности с центром в точке (0;0) и радиусом  R=1 , граница круга не входит в область .

ООФ - это кольцо, то есть  часть плоскости, лежащая между

окружностями с центром в точке (0;0) и радиусами, равными 2 и 1

( окружность х²+у²=4  входит в обл. определения функции, окружность

х²+у²=1  не входит в обл. определения ) .