Помогите с линейной алгеброй 10 баллов
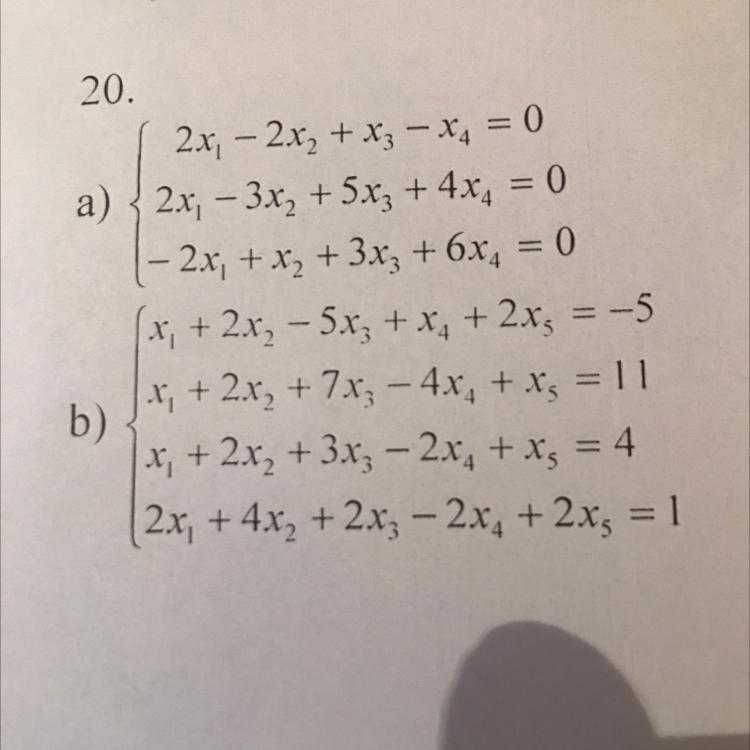
Ответы
Ответ:
Объяснение:
a) СЛУ:
2x₁-2x₂+x₃-x₄=0
2x₁-3x₂+5x₃+4x₄=0
-2x₁+x₂+3x₃+6x₄=0
Решение методом Гаусса:
| 2 -2 1 -1 | 0 | | 0 1 -4 -5 |0| | 0 1 -4 -5 |0|
| 2 -3 5 4 | 0 |=| 2 -3 5 4 |0|=| 0 -2 8 10 |0|=
| -2 1 3 6 | 0 | | -2 1 3 6 |0| | -2 1 3 6 |0|
| 0 0 0 0 |0|
=| 0 -2 8 10 |0|
| -2 1 3 6 |0|
-2x₂+8x₃+10x₄=0 |(-2)
x₂-4x₃-5x₄=0
x₂=4x₃+5x₄
-2x₁+x₂+3x₃+6x₄=0
-2x₁+4x₃+5x₄+3x₃+6x₄=0
-2x₁+7x₃+11x₄=0
-2x₁=-7x₃-11x₄
x₁=-(7x₃+11x₄)/(-2)=(7x₃+11x₄)/2=3,5x₃+5,5x₄
x₃, x₄ - свободные переменные
| 3,5x₃+5,5x₄ |
Ответ: X=| 4x₃+5x₄ |
| x₃ |
| x₄ |
b) СЛУ:
x₁+2x₂-5x₃+x₄+2x₅=-5
x₁+2x₂+7x₃-4x₄+x₅=11
x₁+2x₂+3x₃-2x₄+x₅=4
2x₁+4x₂+2x₃-2x₄+2x₅=1
Решение методом Гаусса:
| 1 2 -5 1 2 |-5| | 0 0 12 -5 -1 |16| | 0 0 12 -5 -1 |16|
| 1 2 7 -4 1 | 11 |=| 1 2 7 -4 1 | 11|=| 0 0 -4 2 0 |-7|=
| 1 2 3 -2 1 | 4 | | 1 2 3 -2 1 | 4| | 1 2 3 -2 1 | 4 |
| 2 4 2 -2 2 | 1 | | 2 4 2 -2 2 | 1| | 2 4 2 -2 2 | 1 |
| 0 0 12 -5 -1 |16|
=| 0 0 -4 2 0 |-7|
| 0 0 -4 2 0 |-7|
| 2 4 2 -2 2 | 1 |
Получились в матрице две одинаковые строки. Так как они идентичны, то одну строку можно убрать.
| 0 0 12 -5 -1 |16 |
| 0 0 -4 2 0 |-7|
| 2 4 2 -2 2 | 1 |
Определим ранг матрицы основной системы A:
| 0 0 12 -5 -1 | | 2 4 2 -2 2 | | 1 2 1 -1 1 |
A=| 0 0 -4 2 0 |=| 0 0 -4 2 0 |=| 0 0 -4 2 0 |=
| 2 4 2 -2 2 | | 0 0 12 -5 -1 | | 0 0 12 -5 -1 |
| 1 2 1 -1 1 | | 1 2 1 -1 1 |
=| 0 0 1 -1/2 0 |=| 0 0 1 -1/2 0 |
| 0 0 12 -5 -1 | | 0 0 0 1 -1 |
Получились три ненулевые строки. Следовательно, ранг A=3.
Теперь определим ранг матрицы расширенной системы B:
| 0 0 12 -5 -1 16 | | 2 4 2 -2 2 1 |
B=| 0 0 -4 2 0 - 7 |=| 0 0 -4 2 0 -7 |=
| 2 4 2 -2 2 1 | | 0 0 12 -5 -1 16 |
| 1 2 1 -1 1 1/2 | | 1 2 1 -1 1 1/2 |
= | 0 0 -4 2 0 -7 |=| 0 0 1 -1/2 0 7/4 |=
| 0 0 12 -5 -1 16 | | 0 0 12 -5 -1 16 |
| 1 2 1 -1 1 1/2 |
=| 0 0 1 -1/2 0 7/4 |
| 0 0 0 1 -1 5 |
Получились три ненулевые строки. Следовательно, ранг B=3.
rang(A)=rang(B) ⇒ данная система совместна.
12x₃-5x₄-x₅=16; 5x₄=12x₃-x₅-16; 10x₄=24x₃-2x₅-32
-4x₃+2x₄=-7; 2x₄=4x₃-7; 10x₄=20x₃-35
2x₁+4x₂+2x₃-2x₄+2x₅=1; 2x₄=2x₁+4x₂+2x₃+2x₅-1; 10x₄=10x₁+20x₂+10x₃+10x₅-5
24x₃-2x₅-32=20x₃-35; 4x₃-2x₅=-3; 2x₅=4x₃+3; x₅=2x₃+1,5
20x₃-35=10x₁+20x₂+10x₃+10x₅-5 |5
2x₃-6=2x₁+4x₂+4x₃+3; 2x₁=-4x₂-4x₃-3-6; x₁=-2x₂-2x₃-4,5
x₄=2x₃-3,5
x₂, x₃ - свободные переменные.
| -2x₂-2x₃-4,5|
Ответ: X=| x₂ |
| x₃ |
| 2x₃-3,5 |
| 2x₃+1,5 |