Предмет: Геометрия,
автор: regina2324
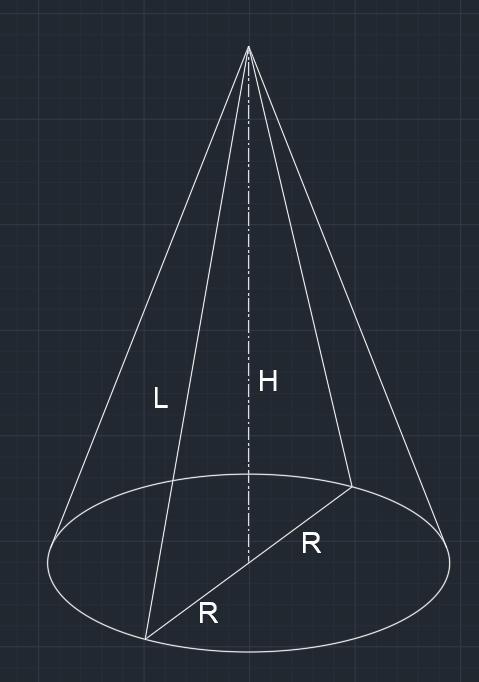
Дан конус. R:H=3:4.Объём конуса равен 96Псм3.Найти а)длину образующей б) площадь осевого сечения
Ответы
Автор ответа:
1
Ответ:
Длина образующей
Площадь осевого сечения
Объяснение:
R:H=3:4
Отсюда R=(3*H)/4
Объём конуса равен
Образующую находим по теореме Пифагора
Площадь осевого сечения
Приложения:
Автор ответа:
0
Ответ:
а) длина образующей равна 10 см
б) площадь осевого сечения конуса 48 см²
Объяснение:
Дано:
R - радиус основания конуса
Н - высота конуса
R : H = 3 :4
V = 96π см³
Найти:
а) L - длину образующей
б) Soc - площадь осевого сечения
Решение:
Объём конуса вычисляется по формуле
По условию
Тогда
Откуда
Тогда
Длина образующей
Площадь осевого сечения
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: rzuangauhar
Предмет: Русский язык,
автор: LUNA5555
Предмет: Русский язык,
автор: Алансупер
Предмет: Биология,
автор: Павлентий855575