Предмет: Математика,
автор: dmitrievadara545
1.Найдите точку минимума функции y=3x^5-5x^3
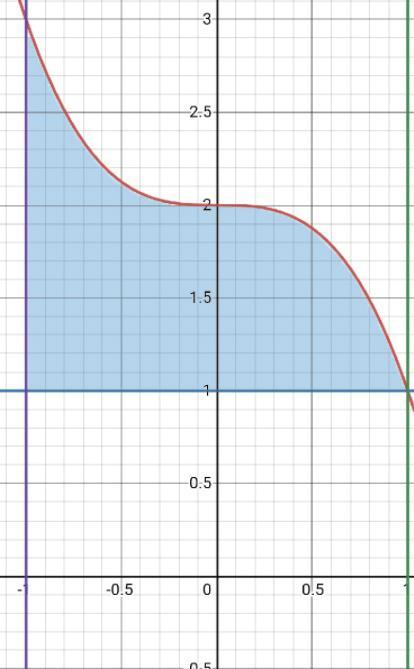
2.Вычислите площадь фигуры (S), ограниченной линиями y=2-x^3 ,y=1 ,x=-1 ,x=1
3.Найдите производную функции f(x)=(4+7x)^3
4.Укажите превообразную функции fx=6x^5+2x^2
Приложения:

Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Фигура изображена на прикреплённом рисунке.
Найдем ее площадь:
Пусть a - общее ребро, а b и с - оставшиеся рёбра первой и второй грани соответственно. тогда:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: олечка72
Предмет: Окружающий мир,
автор: 23021986
Предмет: Русский язык,
автор: marish555
Предмет: Математика,
автор: bahus4099992gmailcom
Предмет: Алгебра,
автор: Аля020304