Предмет: Алгебра,
автор: Gkkcvb
Решите уравнение...............
Приложения:
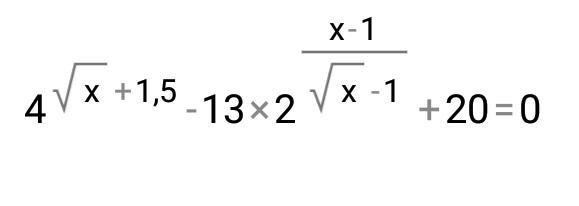
Ответы
Автор ответа:
1
Очень интересное уравнение)
Решение задания прилагаю.
Приложения:

Автор ответа:
1
Ответ:
Объяснение:
При этом не забываем, что ОДЗ x больше или равен нулю, поскольку стоит под корнем и x≠1, поскольку знаменатель в показателе степени будет равен нулю, а на ноль делить нельзя.
Произведём замену
Решаем обыкновенное квадратное уравнение
Производим обратную замену для двух корней
Но этот корень нам не подходит, поскольку не принадлежит ОДЗ
Этот корень удовлетворяет условиям
Похожие вопросы
Предмет: Қазақ тiлi,
автор: АРИАНАалаоао
Предмет: Русский язык,
автор: 564юлия
Предмет: Қазақ тiлi,
автор: нурик53
Предмет: Математика,
автор: Leneyka2223
Предмет: Химия,
автор: знанич65