Помогите решить задания

Ответы
Ответ:
9. Площадь полной поверхности метров квадратных.
10.
Площадь боковой поверхности дециметров квадратных.
Объем дециметров кубических.
Пошаговое объяснение:
9.
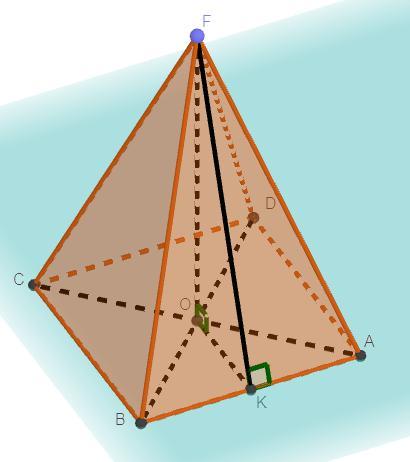
Дано: ABCD - квадрат, AC = 12 м, ∠(FAB, ABCD) = 45°, правильная четырехугольная пирамида FABCD
Найти: S - ?
Решение: Так как по условию ABCD - квадрат, то по свойствам квадрата все его стороны равны, пусть сторона квадрата AB = x, следовательно AB = BC = CD = AD = x. Рассмотрим треугольник ΔABC, который является прямоугольным так как по одному из определений квадрат это ромб с углом 90°, тогда по теореме Пифагора:
м.
К стороне AB проведем апофему в точку K. По свойству правильной четырехугольной пирамиды FABCD, точка F проектируется в центр пересечения диагоналей квадрата. Пусть диагонали квадрата пересекаются в точке O, тогда точка F проектируется в точку O и отрезок FO - высота пирамиды. По свойству квадрата его диагонали равны и точкой пересечения делятся пополам, тогда BD = AC и OA = OC = OD = OB = AC : 2 = 12 : 2= 6м. По теореме о трех перпендикулярах так как, FK ⊥ AB как апофема, OF ⊥ ABCD по построению, то OK ⊥ AB.
Рассмотрим треугольник ΔAOB. Так как AO = OB, то треугольник ΔAOB является равнобедренным. Так как OK ⊥ AB, то OK - высота треугольника ΔAOB проведенная к его основанию AB, следовательно по свойству равнобедренного треугольника высота проведенная к основанию равнобедренного треугольника является биссектрисой и медианой, то есть BK = KA = AB : 2 = x : 2 = м. Рассмотрим прямоугольный треугольник ΔOKA (OK ⊥ AB). По теореме Пифагора:
м.
Угол между двумя плоскостями по определению - это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях, то есть, так как FK ⊥ AB и OK ⊥ AB, то ∠OKF = ∠(FAB, ABCD) = 45°. Рассмотрим прямоугольный треугольник ΔFOK. м.
Пусть площадь боковой поверхности правильной пирамиды .
метров квадратных. Пусть площадь основания пирамиды
, а так как основания пирамиды это квадрат, то по формуле для площади квадрата:
метров квадратных.
метров квадратных.
10.
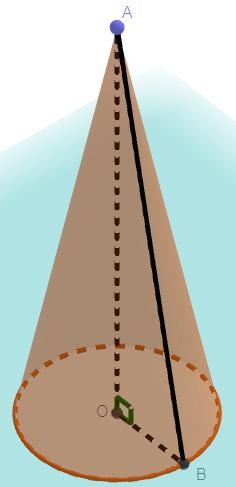
Дано: ∠ABO = 30°, OB = 3 дм, O - центр окружности
Найти: V,S - ?
Решение: По определению отрезок OA - высота конуса так как O - центр окружности которая лежит в основании конуса, тогда треугольник ΔAOB - прямоугольный, следовательно:
дм.
дм.
дециметров квадратных.
дециметров кубических.