Предмет: Математика,
автор: svetabaky6
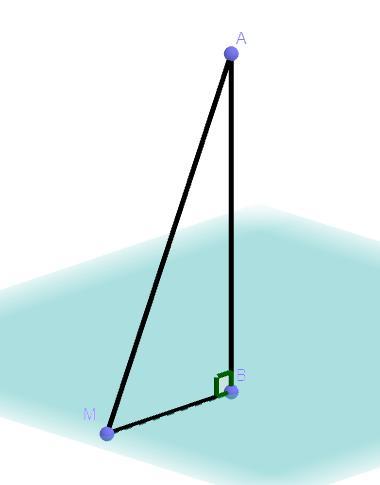
Угол между прямой AM и плоскостью α равен 600. Точка М является точкой пересечения АМ и плоскости α, а точка А точкой пересечения АМ и ее перпендикуляра на плоскость. Найдите длину проекции АМ на плоскость, если АМ=8.
с рисунком
Ответы
Автор ответа:
1
Ответ:
Проекции АМ = MB = 4
Пошаговое объяснение:
Дано: ∠AMB = 60°, AM = 8, MB ⊥ α.
Найти: MB - ?
Решение: Так как по условию MB ⊥ α, то оно перпендикулярно любой прямой лежащей в плоскости α по определению перпендикулярности прямой к плоскости, следовательно AB ⊥ MB .
Рассмотрим треугольник ΔAMB, который является прямоугольным так как AB ⊥ MB, тогда
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: rayana777
Предмет: Окружающий мир,
автор: 1964svetka
Предмет: Русский язык,
автор: catyarocheva
Предмет: Окружающий мир,
автор: Коржик555