Предмет: Алгебра,
автор: budatov99
Логарифм помогите не могу решить никак заранее спасибо)
Приложения:
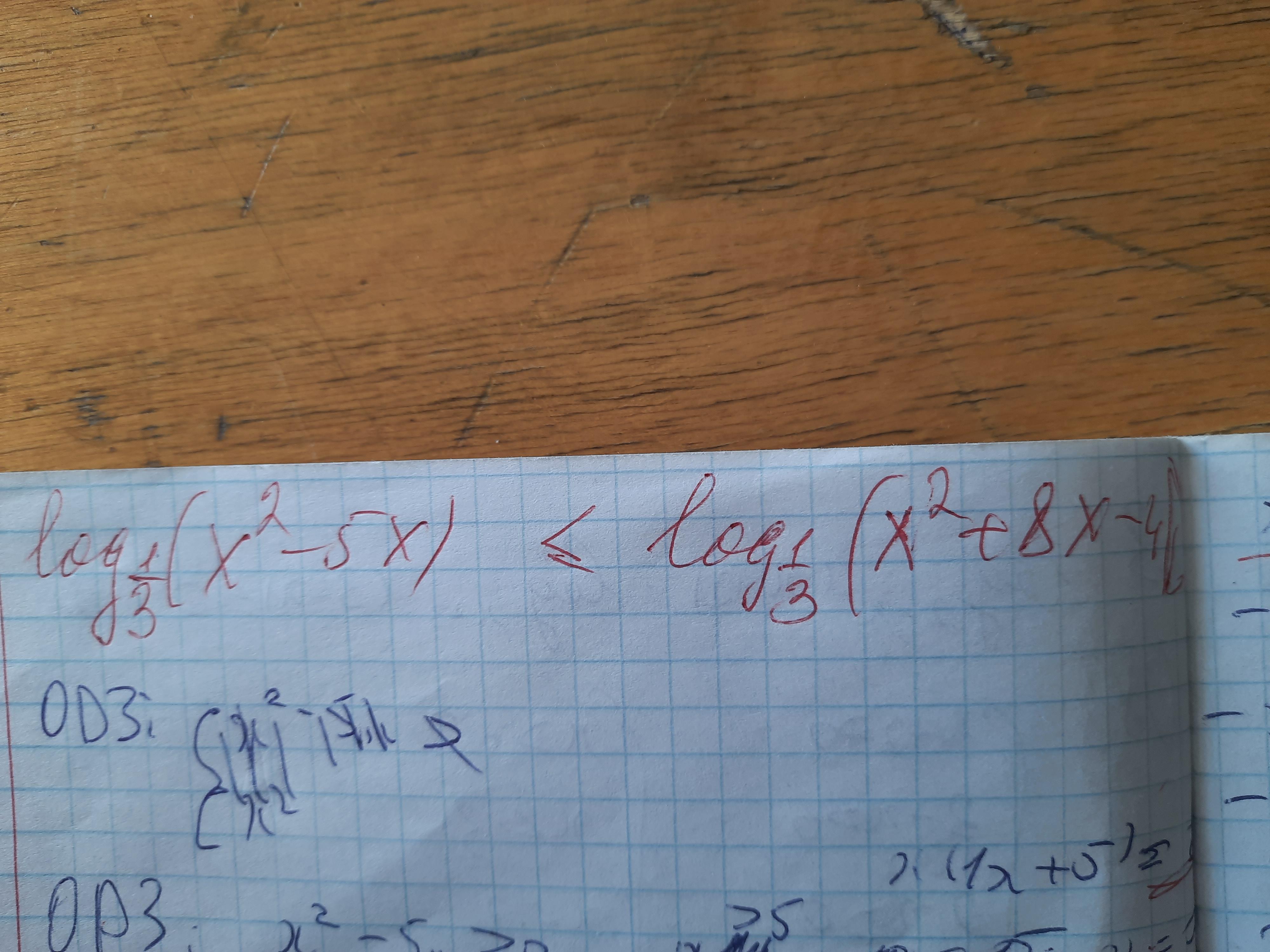
terikovramazan:
решение давно готово, но не могу вставить
Блин решение осень надое
а ответ верный
До меня учитель докапался, незнаю решение
скинь эл.адрес
или подожди, кто то отвечает
budatov99@gmail.com
Ответы
Автор ответа:
1
Ответ: приложен
Объяснение:
Приложения:

А почему поменялся знак от меньше или равно на больше или равно
при делении или умножении уравнения на отрицательное число
у меня есть ошибки при решении, вместо 3/2 должен быть ноль и далеее. я уже не могу исправить
идеально выполнено у
Universalka
Universalka
Автор ответа:
1
ОДЗ :
1) x² - 5x > 0
x(x - 5) > 0
+ + + + + (0)- - - - - (5)+ + + + +
///////////// ////////////
x ∈ ( - ∞ ; 0) ∪ (5 ; + ∞)
2) x² + 8x - 4 > 0
x² + 8x - 4 = 0
D = 8² - 4 * (- 4) = 64 + 16 = 80 = (4√5)²
+ + + + + - 4 - 2√5 - - - - - 2√5 - 4 + + + + +
////////////// //////////////
x ∈ (- ∞ ; - 4 - 2√5) ∪ (2√5 - 4 ; + ∞ )
Окончательно : x ∈ (- ∞ ; - 4 - 2√5) ∪ (5 ; + ∞)
Похожие вопросы
Предмет: Окружающий мир,
автор: Александр1107
Предмет: Окружающий мир,
автор: k210379
Предмет: Қазақ тiлi,
автор: досан2
Предмет: Математика,
автор: Karinaone