Предмет: Алгебра,
автор: pavelnemchev91
область определения функции
Приложения:
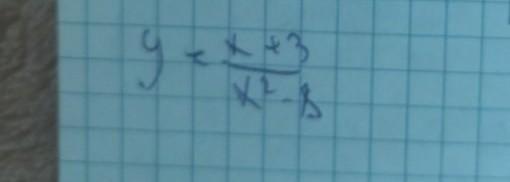
Ответы
Автор ответа:
0
Ответ:
Объяснение:
∪ означает объединение множеств.
Автор ответа:
1
Знаменатель дроби не должен равняться нулю , так как на ноль делить нельзя .
Похожие вопросы
Предмет: Русский язык,
автор: Киска56788
Предмет: Русский язык,
автор: 968756652
Предмет: Русский язык,
автор: robomaks
Предмет: Математика,
автор: сагынбековаэлина1
Предмет: Математика,
автор: Mamedovamadina