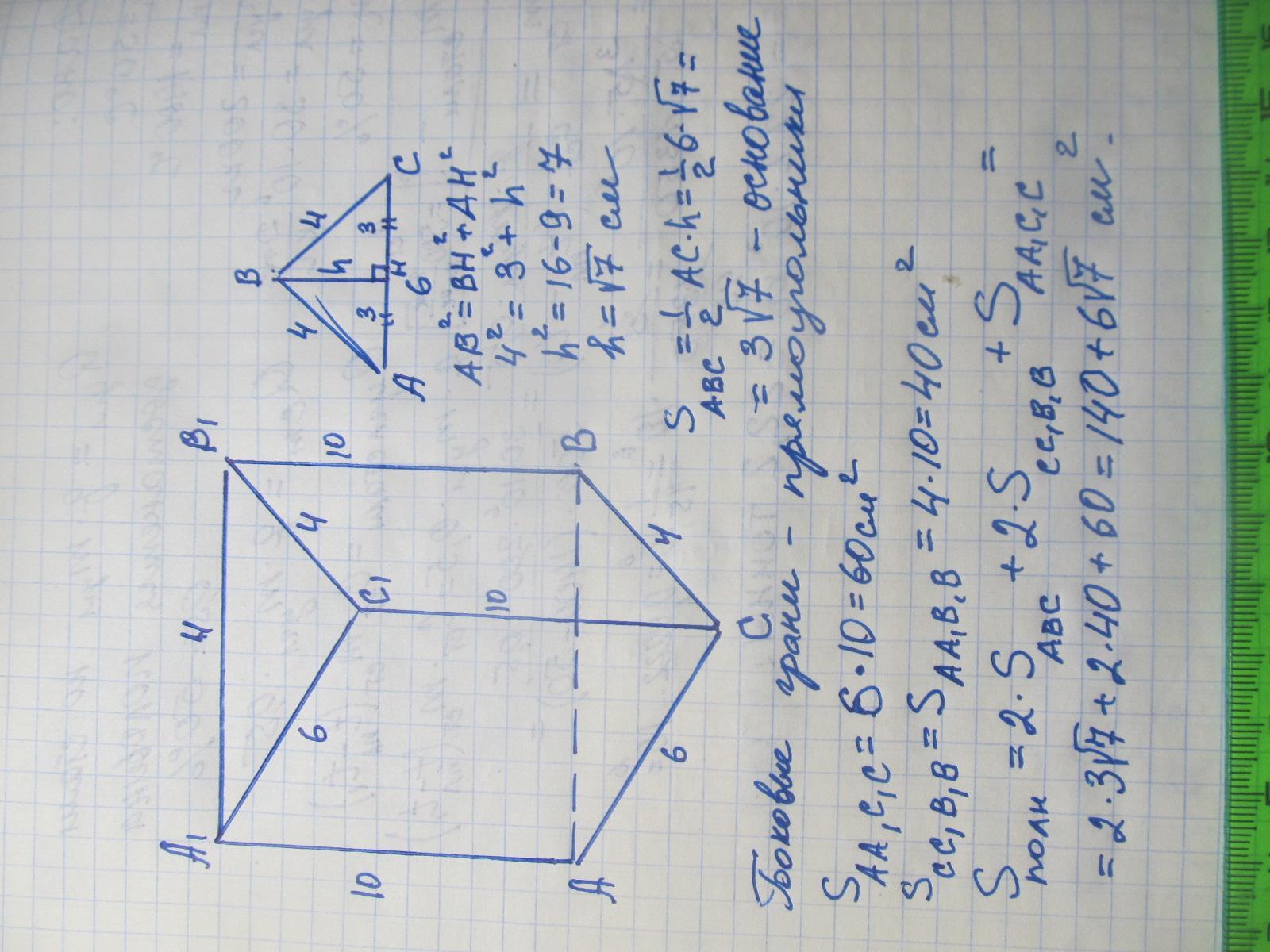
В основании треугольной прямой призмы лежит равнобедренный треугольник с боковой стороной 4 см и основанием 6 см.Боковое ребро призмы равно 10 см.Найдите площади поверхности призмы.
Ответы
Ответ:
S₍осн₎ = 3√7
S₍бок₎ = 140
S₍полн₎ = 140 + 6√7
Объяснение:
Дано: треугольная прямая призма ABCA₁B₁C₁; основание призмы - равнобедренный треугольник со сторонами 4(боковая сторона) и 6(основание); боковое ребро призмы - 10.
________________________________________________________
РЕШЕНИЕ
В основании призмы лежит равнобедренный треугольник. Обозначим его за ΔِABC ( где A - вершина, то есть AB=AC=4 - боковые стороны, BC=6 - основание). Опустим в этом ΔِABC высоту AE ( AE ⊥ BC). По свойству равнобедренного треугольника, высота AE (как высота, опущенная из вершины равнобедренного треугольника на его основание), является {также} медианой (и биссектрисой) и делит основание BC пополам (BE = CE = BC/2 = 6/2 = = 3). Из треугольника ΔAEC ( где ∠AEC = 90° ), по теореме пифагора:
AE² = AC² - CE² ⇒ AE = √(AC² - CE²) = √(4² - 3²) = √(16 - 9) = √7
AE = √7
Находим площадь основания призмы:
S₍осн₎ {как площадь треугольника SΔ} = 1/2 * a * hₐ = 1/2 * BC * AE = 1/2 * 6 * √7 = 3√7
S₍осн₎ = 3√7
Боковые ребра призмы - прямоугольники. Если их обозначить за S₍бок₁₎ = S₍AA₁CC₁₎ = S₍AA₁BB₁₎ и S₍бок₂₎ = S₍BB₁CC₁₎, то
S₍бок₎ = 2S₍бок₁₎ + S₍бок₂₎ = 2*(10 *4) + 10 * 6 = 80 + 60 = 140
S₍бок₎ = 140
Общая же поверхность равняется:
S₍полн₎ = S₍бок₎ + 2S₍осн₎ = 140 + 2*3√7 = 140 + 6√7
S₍полн₎ = 140 + 6√7
*Замечание: в данной задаче (при желании) площадь основания (как площадь треугольника) также можно найти по формуле Геррона.
*Замечание: при решении рекомендуется сделать чертёж: это существенно упростит выполнение задания.
Решение на фото/////