Предмет: Математика,
автор: vasilevartem959
Найти производную функции
Приложения:
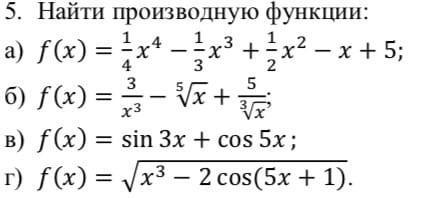
Ответы
Автор ответа:
1
Ответ:
a
б
в
г
Похожие вопросы
Предмет: Русский язык,
автор: KlerVism
Предмет: Українська мова,
автор: kalinka2004
Предмет: Английский язык,
автор: ijnqaz
Предмет: Английский язык,
автор: Серена356798547
Предмет: Русский язык,
автор: Варя1804