Предмет: Алгебра,
автор: akalnemop
Помогите плиз, 1 задание очень просто.
Приложения:

Ответы
Автор ответа:
1
+ + + + + (- 1)- - - - - (3)+ + + + +
//////////////// //////////////
Ответ : x ∈ (- ∞ ; - 1) ∪ (3 ; + ∞)
Автор ответа:
1
Ответ:
Объяснение:
Знаменатель функции должен быть не равным нулю:
√(x²-2x-3)≠0.
Кроме того, подкоренное выражение должно быть больше нуля:
x²-2x-3>0;
Находим нули
x²-2x-3=0;
По т. Виета:
x1+x2=2; x1*x2=-3;
x1=-1; x2=3.
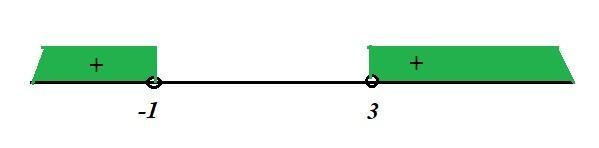
Наносим точки на координатный луч (См. скриншот)
Переходим к неравенству:
Проверяем верность при x=0
0²-2*0-3=-3<0 - не соответствует.
Значит значения x ∈ (-∞;-1)∪(3;+∞).
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Katina052003
Предмет: Русский язык,
автор: 05022007
Предмет: Английский язык,
автор: tonibelenko20
Предмет: Английский язык,
автор: vika2416
Предмет: Другие предметы,
автор: karolina103