Предмет: Алгебра,
автор: Дрындель
Вычислить интеграл
Подробно пожалуйста
Приложения:
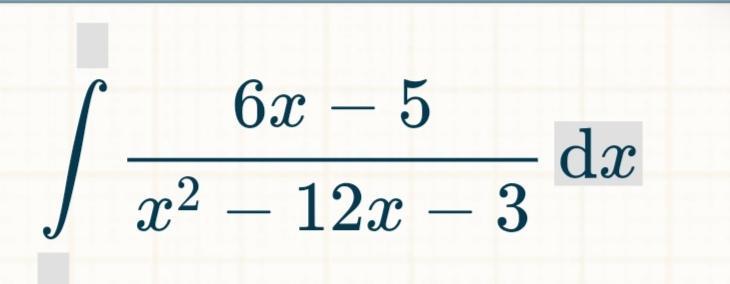
Ответы
Автор ответа:
0
Вычислить интеграл
1. Преобразуем интеграл следующим образом:
2. Разъединим исходную алгебраическую дробь:
3. Разъединим данный интеграл на два:
4. Поработаем с каждым интегралом.
4.1. Рассмотрим первый интеграл. Сделаем замену:
Тогда
Имеем:
4.2. Рассмотрим второй интеграл. Выделим в знаменателе дроби полный квадрат:
Используя формулу имеем:
5. Итоговый результат:
Похожие вопросы
Предмет: Английский язык,
автор: svetlanasvetik2
Предмет: Окружающий мир,
автор: Аноним
Предмет: Английский язык,
автор: stepyirina
Предмет: Английский язык,
автор: anna0111bezborodykh