срочно помогите пожалуйста
Ответы
Ответ:
Объяснение:
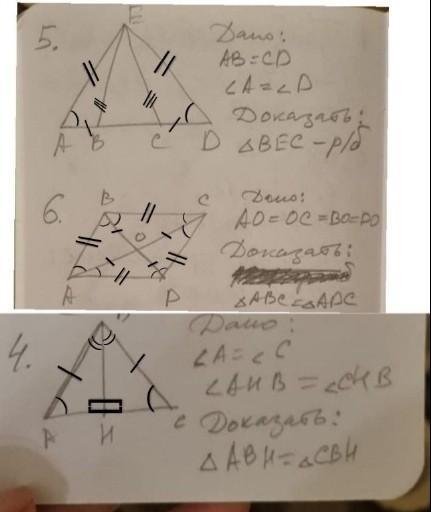
5. ΔАЕВ= ΔДЕС по двум сторонам АВ=СД и АЕ=ДЕ (как стороны равнобедренного ΔАЕД) и углам между ними. Значит стороны ЕВ=ЕД ⇒ ΔВЕС равнобедренный
6. данный четырехугольник - квадрат АС=ВД
диагональ квадрата делит его на равные ΔАВС=ΔАДС
4. ΔАВС равнобедренный ∠А=∠С
∠АНВ+∠СНВ=180° как смежные углы и они равны ⇒ ∠АНВ-∠СНВ=180/2=90° В равнобедренном Δ высота является и медианой ⇒ АН=СН
ΔАВН=ΔСВН по признаку равенства углов ∠А=∠С и равенства прилежащих к этим углам сторон АН=СН и АВ=СВ
Объяснение:
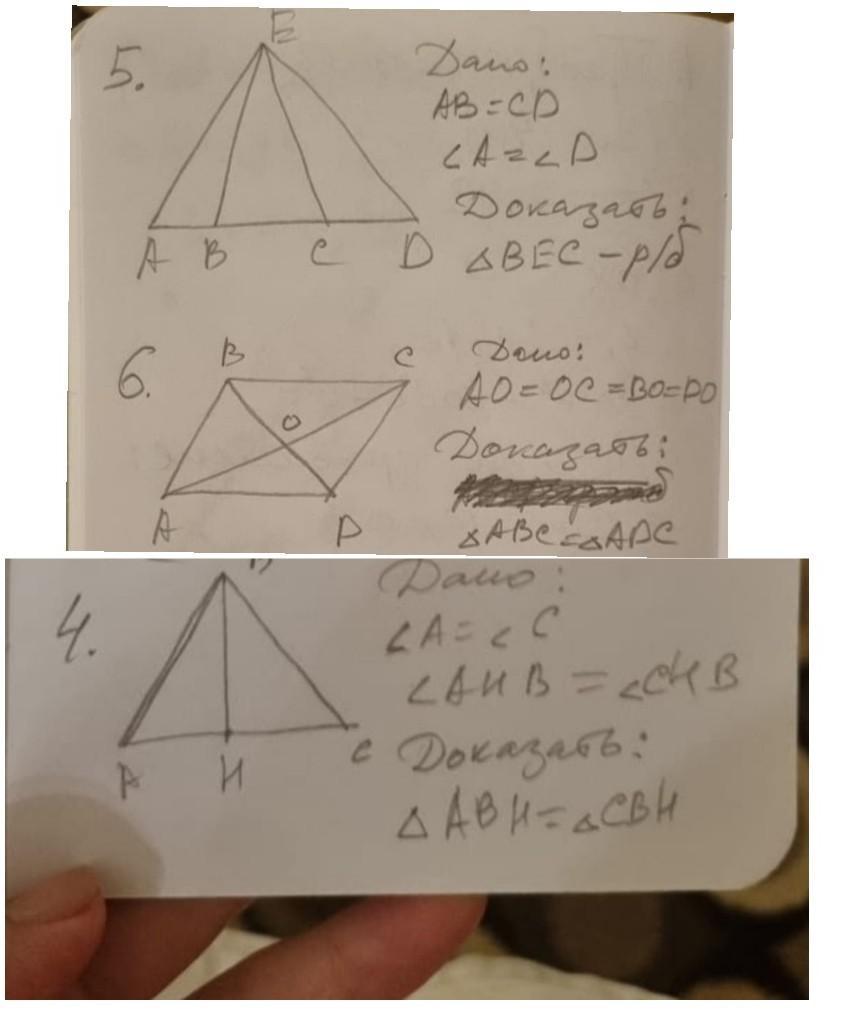
5) Дано :
АВ = СD
∠A = ∠D
Доказать :
△ВЕС — равнобедренный
Доказательство :
1. Т. к. ∠A = ∠D , то △АЕD — равнобедренный
2. △АЕD — равнобедренный , значит АЕ = DE
3. АЕ = DE , ∠A = ∠D , AB = CB , ==> △АЕВ = △СDE — по двум сторонам и углу между ними .
4. Т. к. △АЕВ равен △СDE , то = СЕ
5. ВЕ = СЕ ==>△ВСЕ — равнобедренный , чтд .
6) Дано :
АО = ОС = ВО = PO
Доказать :
△АВС = △АРС
Доказательство :
1. Т. к. АО = ОР , то ∠РАО = ∠ОРА — против равных сторон лежат равные стороны
2. Т. к. ВО = ОС , то ∠ОВС = ∠ОСВ — против равных сторон лежат равные стороны
3. Т. к. АО = ВО , то ∠ОАВ = ∠ОВА — против равных сторон лежат равные стороны
4. Т. к. ОС = ОР , то ∠ОСР = ∠ОРС — против равных сторон лежат равные стороны
5. ∠АВО = ∠АРО = ∠СВО = ∠СРО , ==> ∠СВА = ∠СРА
6. АР = СР
∠СВА = ∠СРА
АВ = ВС , ==> △АВС = △АРС — по двум сторонам и углу между ними , чтд .
4) Дано :
∠ А = ∠C
∠ANB = ∠CBH
Доказать :
△АВН = △СВН
Доказательство:
1. ∠ А = ∠C , значит АВ = ВС — поротив равных углоа лежат равные стороны
2. Т. к. АВ = ВС , то △АВС — равнобедренный
3. Т. к ∠ANB = ∠CBH , то ВН — биссектриса
4. В△АВС ВН — биссектриса и высота — по св. равнобедренного треугольника
5. АВ = ВС
∠ А = ∠C , ==> △АВН = △СВН — по гипотенузе и острому углу , чтд.