Уважаемые эксперты помогите решить три задания, не проходите мимо (задание 9 класс) 30 баллов
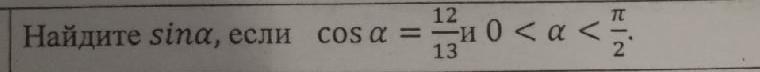

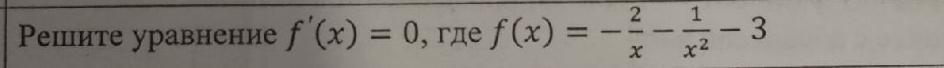
Ответы
Ответ:
Объяснение:
ВОПРОС <1>
cosα = 12/13, при чем 0 < α < π/2 ( т.е. α ∈ ( 0; π/2), или, другими словами, α ∈ Iч {альфа принадлежит первой четверти} )
По основному тригонометрическому тождеству,
sin²α + cos²α = 1
Легко можно вывести sinα:
sin²α = 1 - cos²α
sinα = ±√(1 - cos²α)
Решаем:
sinα = ±√(1 - cos²α) = ± √(1 - (12/13)²) = ±√(1 - 144/169) = ±√(169/169 - 144/169) = ±√((169-144)/169) = ± √ ( 25/169) = ±5/13
У нас получилось два значения: sinα = ±5/13
НО ∠α ∈ ( 0; π/2) [или α ∈ Iч ], а синус угла первой четверти единичной окружности {на координатной плоскости} (ровно как и косинус) положителен, то есть sinα > 0 (ТОЧНЕЕ 0 < sinα < 1 , при 0 < α < π/2 ) а значит, sinα ≠ -5/13
ОТВЕТ: sinα = +5/13
________________________________________________________
ВОПРОС<2>
Дана функция f(x) = 7 - 3x² и требуется найти наименьшее значение функции на отрезке x ∈ [-1 ; 2].
Для начала найдем производную функции, а затем ее критические точки:
f'(x) = (7 - 3x²)' = -3*2x = -6x [следовательно, производная функции f'(x) = -6x. Приравняем её к нулю: ]
-6x = 0 ⇒ x₀ = 0 { - критическая точка}
Проверим, принадлежит ли эта {критическая} точке заданному изначально отрезку: 0 ∈ [-1 ; 2]. Значит берем ее для проверки.
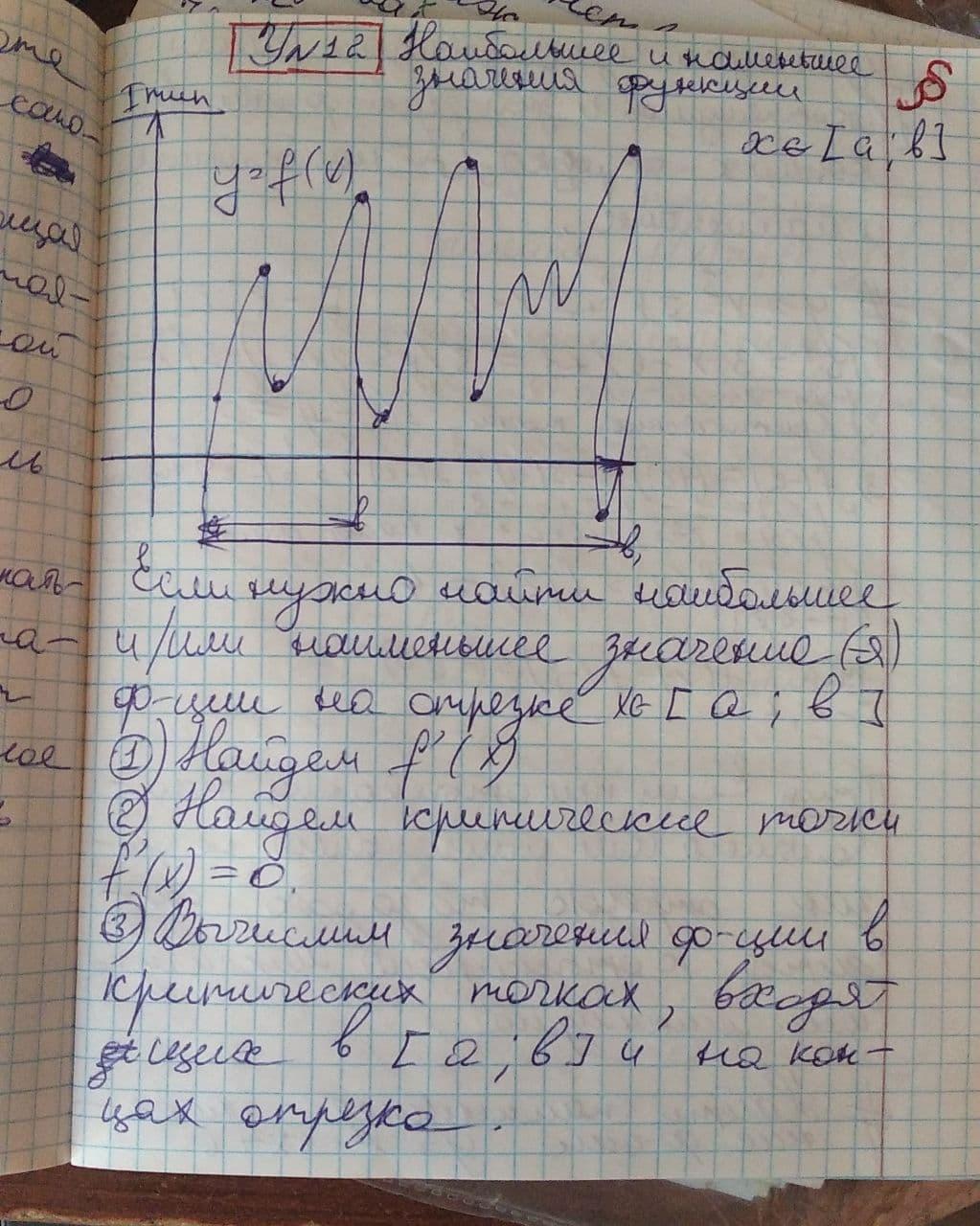
Вспомним-ка...: По правилу, для того, чтобы найти наибольшее (наименьшее) значение функции, необходимо найти ее точки экстремумов, и если они входят в заданный отрезок (в противном случае, они просто - напросто "откидываются"), подставить их, а также крайние точки заданного отрезка в функцию, тем самым рассчитав ее {функции} значения в этих точках. Из полученных значений выбрать наибольшее (наименьшее).
Выполняем:
f(-1) = 7 - 3*(-1)² = 7 - 3 = 4
f(0) = 7 - 3*(0)² = 7 - 0 = 7
f(2) = 7 - 3*(2)² = 7 - 3*4 = 7 - 12 =-5
Сравниваем значения: f(2) < f(-1) < f(0)
-5 < 4 < 7
Значить, f₍наим₎ = -5
ОТВЕТ: f₍наим₎ = -5
________________________________________________________
ВОПРОС<3>
Дано: f(x) = -2/x - 1/x² - 3
Необходимо решить уравнение: f'(x) = 0
Находим f'(x):
f'(x) = (-2/x - 1/x² - 3)' = -2* (-1)*(x⁻²) - 1*(-2)*(x⁻³) = 2/x² + 2/x³
В уравнении f'(x) = 0 заменяем f'(x) на её значение (т.е. на 2/x² + 2/x³
2/x² + 2/x³ = 0
2х/х³ + 2/х³ = 0
( 2х + 2 ) / х³ = 0 ⇒
⇒ 1) 2х + 2 = 0 ⇒ х = -1
и
⇒ 2) х³ ≠ 0 ⇒ х ≠ 0
Следователно, х = -1
ОТВЕТ: х = -1

И Вам спасибо за добрые пожелания